Next we will present the basic formulas that we will use for energy calculations in buildings, such as current, voltage, resistance and power.
Ohm’s Law Formula
We have our Ohm’s Law formula, which is the most used in electrical circuit calculations. Is the next:
V=I\times R
Which V is the voltage or potential difference measured in volts (V); I is the current, intensity or amperage measured in amps (A); R is the resistance measured in ohms \Omega.
First potency formula
We have that our first power formula looks a lot like Ohm’s Law and it is also very easy to remember and apply. Says so:
P = V \times I
Where P is the power or work measured in watts W; and the voltage and current we already saw in the formula before this one.
Second power formula
This formula is very useful when we want to calculate the power but we only have the current and the resistance:
P=I^{2} \times R
And these are all variables that we already know. From now on we will no longer include unknown variables.
Third potency formula
When we have only the voltage and the resistance, this formula saves us from all those occasions to determine its power:
P = \cfrac{V^{2}}{R}
Sum of resistances formula
Remembering the formulas of the resistors, we have two, one is when we have resistors in series and the other formula is when we have resistors in parallel. It is also what we know as series circuits and parallel circuits.
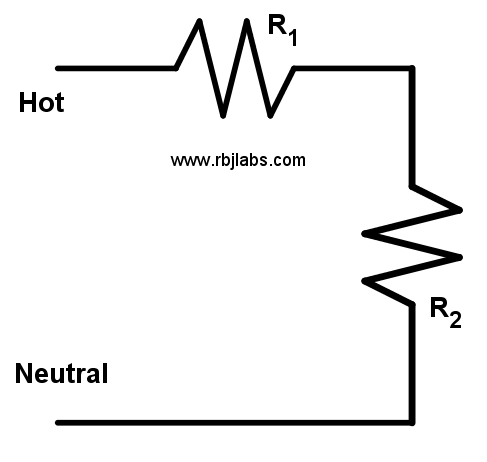 Resistors in series | 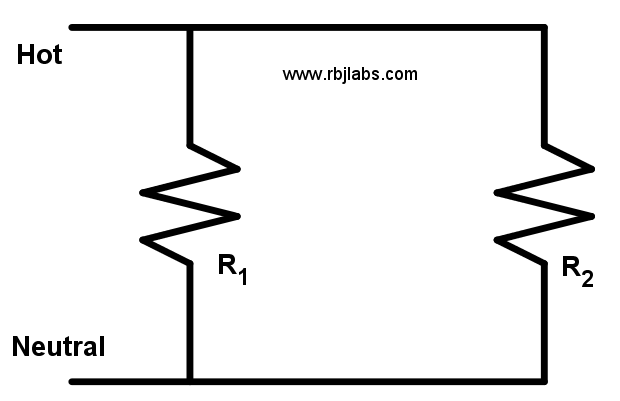 Resistors in parallel |
Series resistor formula
This formula is very simple since all you have to do is add, if you have a resistance with a value and then you have another resistance with the same or another value, add them and voila, you get the value of the total resistance or equivalent resistance R_{T}.
R_{T}=R_{1} + R_{2} + \dots + R_{n}
Parallel Summation Formulas
This formula is a bit more complicated as you have to be careful when leaving the equivalent resistance alone, since the formula is as follows:
\cfrac{1}{R_{T}} = \cfrac{1}{R_{1}} + \cfrac{1}{R_{2}} + \dots + \cfrac{1}{R_{n}}
When you have all the sums of the reciprocals of the resistances you have to clear the R_{T} to get the total resistance.
Thank you for being in this moment with us : )
