Next we will see several exercises of simple electrical installations, I clarify that they are not exercises of electrical circuits as such, they are exercises as if we were to carry out an electrical installation in a building, not as if we were to make a phenolic plate with several more complex circuits.
Exercise 1 of electrical installations
We have the following circuit that powers a lamp and the objective of this exercise is to find the resistance that opposes the passage of current.
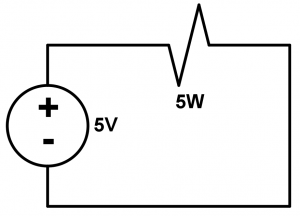
This exercise is very simple, it is a simple formula that we will do, using the following formula the exercise is solved:
P=\cfrac{V^{2}}{R}
And all we have to do is clear the resistance:
R=\cfrac{V^{2}}{P}
Now we simply apply variables that we already have such as the voltage of 5V and the power of the lamp of 5W:
R=\cfrac{(5V)^{2}}{5W} = 5 \Omega
This gives us as a result that the resistance of our lamp is 5\Omega
Exercise 2 of electrical installations
A lamp has a resistance of 181.1\Omega and is connected to the voltage of a house. Taking the average or common voltage of 127V and using the following circuit, what is the wattage of the lamp?
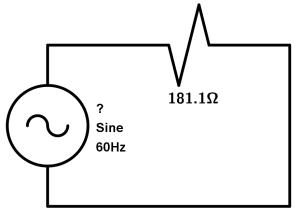
For this exercise we will use the formula from exercise 1 and directly apply the formula:
P=\cfrac{(127V)^{2}}{181.1\Omega }=89.06W
So our lamp power is 89.06W
Keep in mind that in this exercise they gave us other data such as frequency and that it is a sinusoidal. In this type of exercise it does not affect anything that is of a frequency of 50\text{Hz} or 60\text{Hz}, if they are already telling us that the voltage is 127V, it is more than enough for us to be able to solve the exercise.
I’m telling you so that you don’t stress me out because as they see that in an exercise they give you more data, it means that you have to use them.
Exercise 3 of electrical installations
In a series circuit with voltage of 127V and resistors shown in the circuit, calculate the total resistance R_{T}, the current I and the power P.
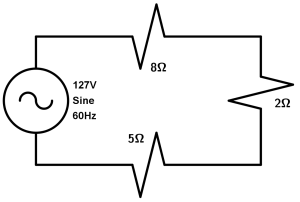
Let’s start with the total resistance, it is simply a sum since there are all the resistors in series, so for our equivalent resistance we have the following:
R_{T} = 8\Omega + 2\Omega + 5\Omega \ \rightarrow R_{T} = 15 \Omega
So we have that our total resistance is equal to 15\Omega
For the intensity we will only apply a simple formula of Ohm’s Law:
I = \cfrac{V}{R} = \cfrac{127V}{15\Omega} = 8.46A
The intensity of the circuit is 8.46A
And for the power we apply a formula with the voltage and intensity that we already have and that we already calculated:
P =127V \times 8.46A = 1074.42W
So our power is 1074.42W
Exercise 4 of electrical installations
Calculate the total current that will flow in the circuit and the voltages of each resistor. At the end check the total voltage by adding the voltages of all the resistors.
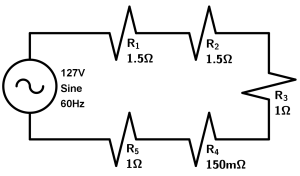
As we did in the previous exercise, since we have that all the resistances are in series, we simply have to add them:
R_{T} = R_{1} + R_{2} + R_{3} + R_{4} + R_{5}
R_{T} = 1.5\Omega + 1.5 \Omega + 1 \Omega + 1 \Omega + 0.15\Omega
The sum gives us an equivalent resistance of 5.15\Omega
Next, what we have to do is apply the Ohm’s Law formula to obtain the total current of the circuit:
I_{T} = \cfrac{127V}{5.15\Omega} = 24.66A
So we have that the total current of the circuit is 24.66A.
In this last step of calculating the voltages of each resistance we will simply have to do several multiplications with the same formula of Ohm’s Law of V = R \times I
V_{R1} = 1.5\Omega \times 24.66A = 36.99V
V_{R2} = 1.5\Omega \times 24.66A = 36.99V
V_{R3} = 1\Omega \times 24.66A = 24.66V
V_{R4} = 0.15\Omega \times 24.66A = 3.69V
V_{R5} = 1\Omega \times 24.66A = 24.66V
When performing all the sums of the resistances, we have the following:
36.99V+36.99V+24.66V+3.69V+24.66V = 126.99V
Exercise 5 of electrical installations
Calculate the total current that will flow through the circuit and the total resistance of the circuit. Remember that the total resistance of the circuit must be less than the partial resistances.
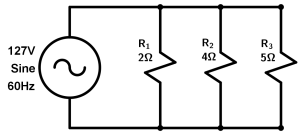
To begin, the formula that we will use is that of the sum of the resistances in parallel, you can see it by clicking here. So let’s get started:
\cfrac{1}{R_{T}} = \cfrac{1}{2} + \cfrac{1}{4} + \cfrac{1}{5} = \cfrac{10}{20} + \cfrac{5}{20} + \cfrac{4}{20} = \cfrac{19}{20}
Now that we have the total, we need to solve for our equivalent resistance of the parallel circuit:
\cfrac{1}{R_{T}} = \cfrac{19}{20} \ \rightarrow \ R_{T} = \cfrac{20}{19} = 1.05\Omega
So our equivalent resistance is equal to 1.05 \Omega.
And simply to calculate the intensity of our source, we apply the Ohm’s Law formula with the intensity cleared:
I=\cfrac{127V}{1.05\Omega} = 120.95A
Finally we have that our circuit current is 120.95A.
Exercise 6 of electrical installations
Calculate the total resistance of the circuit, the total current, and the power that will flow. Check by calculating the partial currents and adding them.
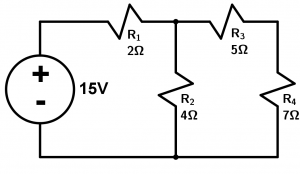
To start with this exercise, what we will do is add resistance 3 with resistance 4 because they are in series, which gives us a value of 12 \Omega.
Next we have to calculate the equivalent resistance of the 12 \Omega with resistance 2 adding in parallel:
\cfrac{1}{R_{T}} = \cfrac{1}{12} + \cfrac{1}{4} = \cfrac{1}{12} + \cfrac{3}{12} = \cfrac{4}{12} =\cfrac{1}{3} \rightarrow R_{2,3,4} = 3\Omega
Now we have to add the equivalent resistance with resistance 1, as they are in series, we will have a total resistance of 5\Omega.
The current is simply calculated with Ohm’s Law:
I=\cfrac{V}{R} = \cfrac{15V}{5\Omega}=3A
So our current is 3A.
We calculate the voltage of resistor 1:
V_{R1} = 2\Omega \times 3A = 6V
The voltage of resistors 2, 3 and 4 is the difference of the total with the calculated one, that means that it is 9V. Letting us understand that the voltage across resistor 2 is 9V and the voltage across the equivalent resistor 3 and 4 is also 9V.
Since we already have the voltages, we simply have to find the currents that will flow in resistor 2 and in the equivalent resistor of 3 and 4. We simply use Ohm’s Law:
I_{R2} = \cfrac{9V}{4\Omega } = 2.25A \qquad I_{R3,4} = \cfrac{9V}{12\Omega} 0.75A
Adding these two resistors we obtain a value of 3A, giving us the same value as the total current of the circuit, which means that the calculations of both equivalent resistors and the current flowing in certain resistors are correct.
Thank you for being in this moment with us : )
