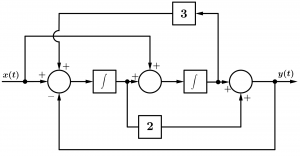
Starting to study the way to find the transfer function of a block diagram in control systems you can find that you have to reduce by blocks until you have only one block to find the transfer function, this is a bit complicated when you have a block diagram with many components. Let me tell you that finding the transfer function is much easier when we use pure equations and we forget the diagram for a while, this is what I am going to explain in this article, we go straight with the example.
Calculate the transfer function of the following block diagram
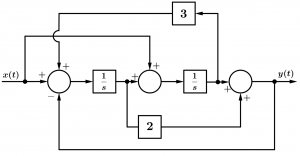
For the integrals that are in the diagram, we must consider Laplace because the Laplace transform of the integrals in our diagram are equal to \frac{1}{s}, replace in the diagram:
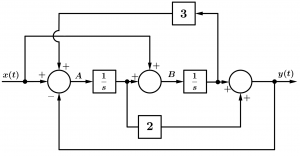
What we will do next will be to name the outputs of the comparators (the circles):
As you can see in the previous diagram, we add names to the outputs, now that we have the output A and the output B, we will raise the equations.
Let’s put the equation for the A exit. The first part of the equation involves the profit of 3, the block of \frac{1}{s} and the output of B, and it is considered as if all those components were linked in series, so remember that the blocks that are connected in series multiply. Then you have to add the x entry. Finally we have to subtract the output y (which in reality we will consider it as an input) to obtain our equation for the output A:
A = \cfrac{3B}{s} + x - y
Let’s put the equation for the B exit. One of these entries includes the x entry, the other entry is added where A multiplies \frac{1}{s} since they are considered to be connected in series and the equation is:
B = x + \cfrac{A}{s}
We go with the equation of the output y. The output y has two entries, one of those entries is the multiplication of the output B for the block \frac{1}{s}, then you have to add the other entry which includes the gain 2, a \frac{1}{s} and the output A, are considered to be connected in series and multiply, let’s see how the equation of y is:
y = \cfrac{B}{s} + \cfrac{2A}{s}
Now comes the part that will perhaps be the most tedious, the part where many are often confused, yes, the part of algebra comes. All you have to do now is get \frac{y}{x} to find our transfer function which should only have s terms. Let’s start.
What we did first was replace the B in the A equation:
A = \cfrac{3}{s} \left( x + \cfrac{A}{s} \right) + x - y
We multiply the parenthesis:
A = \cfrac{3x}{s} + \cfrac{3A}{s^{2}} + x - y
We spend subtracting the fraction that has the A:
A - \cfrac{3A}{s^{2}} = \cfrac{3x}{s} + x - y
We factor the A and make the sum of the fraction where there are no A terms:
A\left( 1 - \cfrac{3}{s^{2}}\right)= \cfrac{3x + sx - sy}{s}
We solve the sum of the parentheses:
A\left(\cfrac{s^{2}-3}{s^{2}} \right) = \cfrac{3x + sx - sy}{s}
We cancel a s from the denominators and we pass dividing the s^{2}-3 and multiplying the s:
A = \cfrac{(3x + sx - sy)s}{s^{2} - 3}
Great, we already have the equation of A, this equation we will replace it in the A of the equation of B to leave the equation of B equaled to something that only has terms of x, y and s (which is the same as we did to find A):
B = x + \cfrac{1}{s} A = x + \cfrac{1}{s} \left( \cfrac{(3x + sy - sy)s}{s^{2} - 3} \right)
We cancel the s and we will have the equation of B with terms of x, y and s:
B = x + \cfrac{3x + sx - sy}{s^{2} - 3}
With the new A and B equations, we substitute in the equation of y:
y = \cfrac{B}{s} + \cfrac{2A}{s}
y = \cfrac{1}{s} \left(x + \cfrac{3x + sx - sy}{s^{2} - 3} \right) + \cfrac{2}{s} \left( \cfrac{(3x + sx - sy)s}{x^{2} - 3} \right)
We will multiply the fraction of \frac{1}{s} and \frac{2}{s}:
y = \cfrac{x}{s} + \cfrac{3x + sx - sy}{s(s^{2} - 3)}+ \cfrac{6x + 2sx - 2sy}{s^{2} - 3}
What we will do now is to separate the fractions so that they are many fractions sums and we can have fractions that have a monomial in the numerator that only have x and y, it does not matter if they are or are not accompanied by s , s(s^{2}-3) which is equal to s^{3}-3s was also multiplied:
y = \cfrac{x}{s} + \cfrac{3x}{s^{3} - 3s} + \cfrac{sx}{s^{3} - 3s} - \cfrac{sy}{s^{3} - 3s} + \cfrac{6x}{s^{2} - 3} + \cfrac{2sx}{s^{2} - 3} - \cfrac{2sy}{s^{2} - 3}
Now what we will do is pass all the y on one side of the equality and we will leave the x on the other side of the equality:
y + \cfrac{sy}{s^{3} - 3s} + \cfrac{2sy}{s^{2} - 3} = \cfrac{x}{s} + \cfrac{3x}{s^{3} - 3s} + \cfrac{sx}{s^{3} - 3s} + \cfrac{6x}{s^{2} - 3} + \cfrac{2sx}{s^{2} - 3}
We will factor the x and the y:
y\left(1 + \cfrac{s}{s^{3} - 3s} + \cfrac{2s}{s^{2} - 3} \right) = x\left( \cfrac{1}{s} + \cfrac{3}{s^{3} - 3s} + \cfrac{s}{s^{3} - 3s} + \cfrac{6}{s^{2} - 3} + \cfrac{2s}{s^{2} - 3}\right)
What we will do in the parentheses where the y is, is to do the sum of fractions and in the parenthesis where the x is we will add only the fractions that have the same denominators:
y\left( \cfrac{(s^{2} - 3)(s^{3} - 3s) + (s^{2} - 3)(s) + (s^{3} - 3s)(2s)}{(s^{2} - 3)(s^{3} - 3s)} \right) = x\left( \cfrac{1}{s} + \cfrac{3 + s}{s^{3} - 3s} + \cfrac{6 + 2s}{s^{2} - 3} \right)
For the moment we are going to take the equation separately, let’s simplify first the parenthesis of the side where the y are, multiply the parentheses of the numerator:
y\left( \cfrac{s^{5} - 3s^{3} - 3s^{3} + 9s + s^{3} - 3s + 2s^{4} - 6s^{2} }{(s^{2} - 3)(s^{3} - 3s)} \right) =
Let’s add and subtract terms:
y\left( \cfrac{s^{5} + 2s^{4} - 5s^{3} - 6s^{2} + 6s}{(s^{2} - 3)(s^{3} - 3s)} \right) =
Now let’s take the side of the equation where we have the parenthesis where x is found, let’s make the addition of fractions:
= x\left( \cfrac{(s^{3} - 3s)(s^{2} - 3) + s(3 + s)(s^{2} - 3) + s(s^{3} - 3s)(6 + 2s)}{s(s^{3} - 3s)(s^{2} - 3)}\right)
Multiplying the parentheses of the numerator, we will have:
= x\left( \cfrac{s^{5} - 3s^{3} - 3s^{3} + 9s + 3s^{3} - 9s + s^{4} - 3s^{2} + 6s^{4} + 2s^{5} - 18s^{2} - 6s^{3}}{s(s^{3} - 3s)(s^{2} - 3)}\right)
Let’s reduce terms:
= x \left( \cfrac{3s^{5} + 7s^{4} - 9s^{3} - 21s^{2}}{s(s^{3} - 3s)(s^{2} - 3)} \right)
Now that we have the smallest possible fractions, let’s write the whole equation again:
y\left( \cfrac{s^{5} - 2s^{4} - 5s^{3} - 6s^{2} + 6s}{(s^{2} - 3)(s^{3} - 3s)} \right) = x \left( \cfrac{3s^{5} + 7s^{4} - 9s^{3} - 21s^{2}}{s(s^{3} - 3s)(s^{2} - 3)} \right)
We cancel the binomials of the denominators:
y\left( s^{5} - 2s^{4} - 5s^{3} - 6s^{2} + 6s \right) = x \left( \cfrac{3s^{5} + 7s^{4} - 9s^{3} - 21s^{2}}{s} \right)
What we will do now is pass dividing the x to y and the polynomial of the parentheses where y will be passed by dividing:
\cfrac{y}{x} = \cfrac{3s^{5} + 7s^{4} - 9s^{3} - 21s^{2}}{s(s^{5} - 2s^{4} - 5s^{3} - 6s^{2} + 6s)}
We will factor an s^{2} in the polynomial of the numerator and factoring s in the denominator we multiply it with the s that we already had so that it is s^{2} in the denominator:
\cfrac{y}{x} = \cfrac{s^{2}(3s^{3} + 7s^{2} - 9s - 21)}{s^{2}(s^{4} + 2s^{3} - 5s^{2} - 6s + 6)}
We cancel the s^{2}:
\cfrac{y}{x} = \cfrac{3s^{3} + 7s^{2} - 9s - 21}{s^{4} + 2s^{3} - 5s^{2} - 6s + 6}
From here we pay a little more attention, we are going to make a factorization that is not usually done, we will rearrange the terms of the numerator and the denominator:
\cfrac{y}{x} = \cfrac{3s^{3} - 9s + 7s^{2} - 21}{s^{4} - 3s^{2} + 2s^{3} - 6s - 2s^{2} + 6}
Next, what we will do is factorize what is necessary to make us have a binomial (s^{2} - 3) in each addition and subtraction:
\cfrac{y}{x} = \cfrac{3s(s^{2} - 3) + 7(s^{2} - 3)}{s^{2}(s^{2} - 3) + 2s(s^{2} - 3) - 2(s^{2} - 3)}
This is the moment where we will do the factorization not very usual, it is very easy to understand it, we consider that (s^{2}-3) is another letter or thing, let’s call (s^{2}-3) the term happy face (\text{c:}), then we are going to rewrite the equation substituting (s^{2}-3) for the term happy face (\text{c:}):
\cfrac{y}{x} = \cfrac{3s (\text{c:}) + 7(\text{c:})}{s^{2}(\text{c:}) + 2s(\text{c:}) - 2(\text{c:})}
Now it’s easier to understand, factor the term happy face to get the following:
\cfrac{y}{x} = \cfrac{(\text{c:})(3s+7)}{(\text{c:})(s^{2} + 2s - 2)}
Replace the term happy face with (s^{2}-3):
\cfrac{y}{x} = \cfrac{(s^{2} - 3)(3s+7)}{(s^{2} - 3)(s^{2} + 2s - 2)}
We cancel the binomials of (s^{2}-3):
\cfrac{y}{x} = \cfrac{(3s+7)}{(s^{2} + 2s - 2)}
And finally we have calculated our transfer function for the block diagram!
\cfrac{y}{x} = \cfrac{3s + 7}{s^{2} + 2s - 2}
Note:
The tricky thing to calculate the transfer function for these block diagrams is actually the algebra, you have to be careful with some sign or with some number that we do not place or forget out there on the way, but in itself it’s simple, quiet. If you want to know more about these topics you can read the following book:
Ogata, K. (2003). Modern control engineering, One LakeStreet, Upper Saddle River, New Jersey: Pearson Educación, Inc.
Thank you for being at this moment with us:)