La convolución es la función que se obtiene de una cuenta de dos funciones, cada quien le da la interpretación que desee. En esta entrada veremos un ejemplo del caso de convolución continua y un ejemplo del caso análogo o convolución discreta.
Ejemplo de convolución en el caso continuo
El caso continuo requiere integrales para realizar la mismísima convolución y la fórmula de la convolución del caso continuo es:
\displaystyle y(t) = x(t)*h(t) \equiv \int_{-\infty}^{\infty}x(\tau)h(t - \tau) d\tau
Pero no te asustes, vamos a verlo sencillo con un ejemplo.
Veamos las siguientes señales con las que trabajaremos en la convolución:
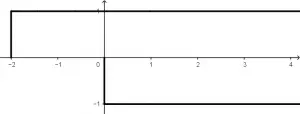
x(t) = \left [u(t + 1) - u(t - 1) \right ] t
h(t) = \left[ u(t + 2) - u(t) \right ]
Nosotros queremos hallar la convolución siguiente:
y(t) = x(t)*h(t)
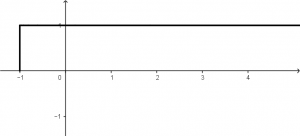
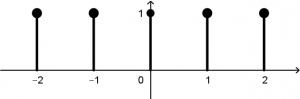
Se graficarán las dos señales para tener una mejor visualización con lo que vamos a trabajar. Vamos a graficar paso a paso las dos señales, empezaremos con la señal de x(t) con lo del interior de los corchetes. La gráfica de u(t+1) es una función escalón, lo que quiere decir que la gráfica se vería de la siguiente manera:
Ahora graficaremos -u(t - 1)
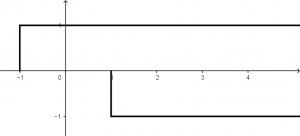
Después de visualizar cómo se vería cada señal por separado, se procederá a colocarlas juntas en una misma gráfica:
Entonces, a la función u(t + 1) se le sumará (o restará, como le entiendas) la función de -u(t - 1) , dando como resultado la siguiente señal:
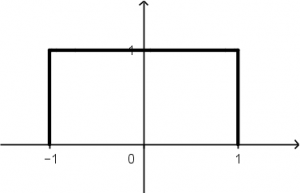
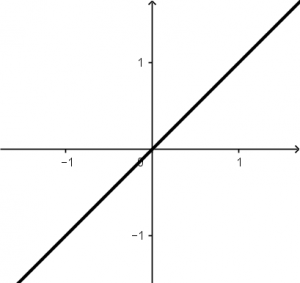
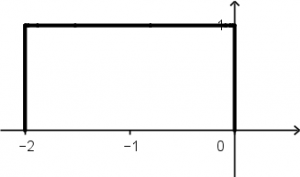
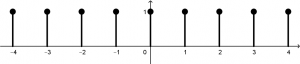
Recordemos que la señal estará multiplicada por t , la cual su gráfica de t es la siguiente:
La multiplicación de la función u(t + 1) - u(t - 1) con t dará como resultado la siguiente señal:
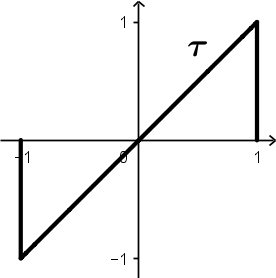
Como esta es la señal que NO se va a desplazar, es a la que se le cambiarán todas sus t por \tau porque la gráfica de la señal es t con pendiente 1, entonces a partir de ahora la señal será \tau .
¡Ya tenemos la primera señal graficada!
Sólo falta graficar la segunda señal, veamos su función:
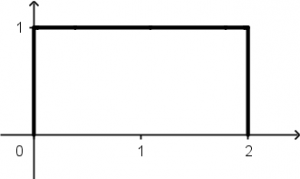
h(t) = \left[ u(t + 2) - u(t) \right ]
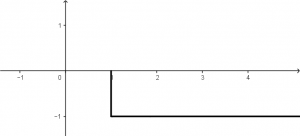
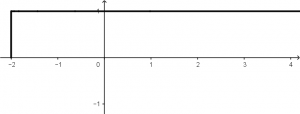
La función escalón u(t + 2) tendrá una gráfica que se observará de la siguiente manera:
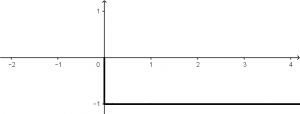
Y la función escalón -u(t) tendrá una gráfica como la siguiente:
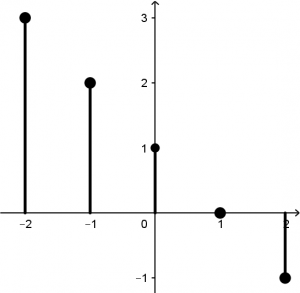
Juntaremos las dos funciones escalón para visualizarlas en una misma gráfica:
Entonces al momento de unir la función escalón u(t + 2) con la función escalón -u(t) tendremos como resultado la siguiente señal:
¡Vamos a convolucionar!
Como lo que nosotros queremos hacer es la convolución y(t) = x(t) * h(t) , entonces la segunda señal es a la que hay que hacerle los ajustes ¿qué quiere decir? Que la segunda señal es la que se va a invertir y es a la que se le va a hacer el cambio de variable.
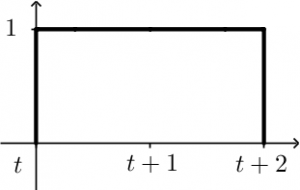
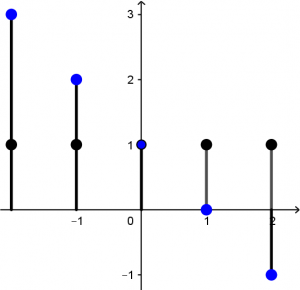
Primero vamos a invertirla, quedaría de la siguiente manera:
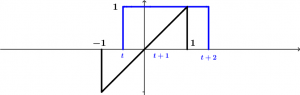
Ahora, en x = 0 se considerará como t , en x = 1 se considerará como t + 1 y en x = 2 se le considerará como t + 2 , veámoslo más gráfico:
¡Ha llegado el momento de hacer los cálculos de la convolución!
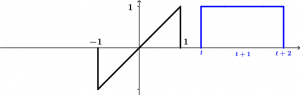
Vamos a colocar la señal \left[ u(t + 2) - u(t) \right ] cuando t < -3 :
No tiene caso realizar integral alguna porque en todo ese instante cuando t < -3 el resultado siempre dará cero.
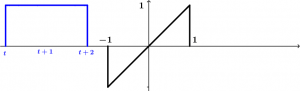
Ahora analicemos el caso cuando la señal \left[ u(t + 2) - u(t) \right ] está entrando en la señal \left [u(t + 1) - u(t - 1) \right ] t , gráficamente se verá así:
Los límites de las integrales de la convolución siempre son de la parte donde están interactuando las dos señales. A nuestra integral de convolución no le podemos colocar límites de t a -1 porque es claro que hay una parte donde las señales no interactúan, por lo tanto, los límites de nuestra integral de convolución tendrías que ir de -1 a t + 2, esos límites se mantendrán en -3 \le t < -1 y como ya sabeos … lo que se integrará será el producto de las dos señales:
\displaystyle-3 \le t < -1 \qquad y(t) = \int_{-1}^{t + 2}(1)(\tau) \ d \tau
Resolvamos la integral:
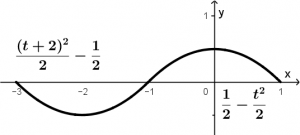
\displaystyle y(t) = \int_{-1}^{t + 2}(1)(\tau) \ d \tau = \int_{-1}^{t + 2}\tau \ d \tau = \left. \cfrac{\tau^{2}}{2}\right |_{-1}^{t + 2} = \underline{\underline{\cfrac{(t + 2)^{2}}{2} - \cfrac{1}{2}}}
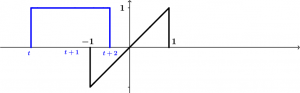
La siguiente integral de convolución se va a realizar desde el momento en el que el punto t de \left[ u(t + 2) - u(t) \right ] ya pasó al -1 de la señal \tau. Gráficamente se verá así:
Como ya se había mencionado, en nuestros límites de integración deben de ir en los momentos en los que interactúan las dos señales. Eso quiere decir que los límites de nuestra siguiente integral irán de t a 1, esto pasa cuando -1 \le t \le 1, veamos:
-1 \le t < 1 \qquad y(t) = \int_{t}^{1}(\tau)(1) \ d\tau
Resolvamos la integral:
\displaystyle y(t) = \int_{t}^{1}(\tau)(1) \ d\tau = \int_{t}^{1}\tau\ d\tau = \left. \cfrac{\tau^{2}}{2}\right|_{t}^{1} = \underline{\underline{\cfrac{1}{2} - \cfrac{t^{2}}{2}}}
Ahora … cuando t > 1 cualquier integral que hagamos, dará como resultado 0 porque no están interactuando las señales. ¿Por qué no están interactuando? Porque la señal \left[ u(t + 2) - u(t) \right ] ya salió de la señal \tau, observa:
Como paso final, graficaremos la convolución. Eso se realiza tomando el resultado que se obtuvieron en las integrales:
¡Y listo, esa sería la convolución de las dos señales!
Convolución en el caso discreto o análogo
La convolución discreta es muy parecida al del caso continuo, ¡incluso es muchísimo más simple! Sólo hay que hacer sumas de multiplicaciones, en un momento lo vemos, primero veamos la fórmula para calcular la convolución en el caso discreto o análogo:
\displaystyle y[n] = x[n] * h[n] = \sum_{k = -\infty}^{\infty}x[k]h[n - k]
Para el ejemplo de la convolución del caso discreto, utilizaremos las siguientes señales:
x[n] = \left ( u[n + 2] - u[n - 3] \right )\left ( 1 - n \right )
h[n] = u[n + 4] - u[n - 5]
Nosotros queremos hallar la siguiente convolución:
y[n] = x[n] * h[n]
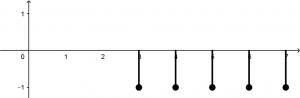
Graficaremos primero la señal x[n] = \left ( u[n + 2] - u[n - 3] \right )\left ( 1 - n \right ). Vamos por partes, la gráfica de la función escalón u[n+2] empezará en x = -2 hasta el infinito con un pulso de altura 1:
La gráfica de la función escalón -u[n - 3] empezará en x =3 hasta el infinito:
Juntamos las dos funciones en una misma gráfica y se observará de la siguiente manera:
Como se pudo observar, cuando las dos funciones hacen contacto en x = 3, se van a tener que sumar (o restar, como le entiendas). Entonces, cuando el pulso de una es de altura 1 y la de la otra señal es de -1, la operación será: 1 - 1 = 0. Eso quiere decir que en x = 3 hasta el infinito, el valor de la suma de las dos señales será igual a cero. Lo que dará como resultado la siguiente señal:
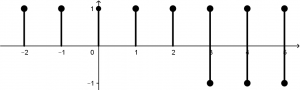
Recordemos que la señal estaba multiplicada por (1 - n), la cual (1 - n) se ve de la siguiente manera:
Entonces nuestra señal \left ( u[n + 2] - u[n - 3] \right ) se multiplicará por cada altura de la recta (1 - n). Eso quiere decir que 3 se multiplicará por 1, 2 se multiplicará por 1, 1 se multiplicará por 1, 0 se multiplicará por 1 y -1 se multiplicará por 1:
Entonces nuestra señal final será:
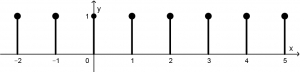
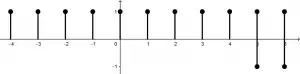
Ahora grafiquemos la señal h[n] = u[n + 4] - u[n - 5]. Empezamos con la gráfica de u[n + 4], la cual se comenzará a graficar en x = -4 hasta el infinito:
Ahora la gráfica de -u[n - 5], la cual se empezará a graficar en x = 5 hasta el infinito:
Juntando las dos gráficas, se visualizarán de la siguiente manera:
Lo que hay que hacer es sumar (o restar, como le entiendas) las gráficas, lo cual quedará de la siguiente manera:
Ahora hay que invertir la segunda señal con respecto al eje y, la cual la señal se verá exactamente igual y además hay que cambiar los números de las posiciones de la señal por n‘s, veámoslo más claro:
¡Ahora sí ya podemos comenzar a convolucionar!
En el caso discreto no hay integrales, sólo hay que multiplicar y sumar, así de simple es.
Primero analicemos el caso cuando las dos señales no se han encontrado, eso quiere decir cuando n < -6:
Lo que se puede observar es que las señales no se han encontrado ¿qué quiere decir? Que por el momento el resultado que vamos a obtener es igual a cero, así que:
\text{cuando } n < -6 \qquad y[n] = 0
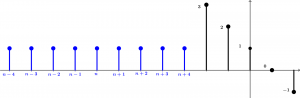
Ahora, cuando n = -6 el resultado ca a ser y[n] = 3, veamos la gráfica:
Al momento en que la señal u[n + 4] - u[n - 5] entra en la señal \left ( u[n + 2] - u[n - 3] \right )\left ( 1 - n \right ) se empieza a multiplicar. Por lo tanto, cuando el pulso de n + 4 de la señal h[n] toca el pulso de altura 3 de la señal x[n], se multiplicará: 1 \cdot 3 = 3. Continuemos…
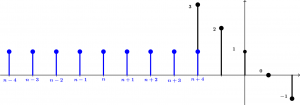
Cuando n = -5 el resultado será y[n] = 5 debido a que en ese momento dos pulsos están teniendo contacto, veamos:
Así que el pulso de n + 4 se va a multiplicar por el pulso de altura 2 y el pulso de n + 3 se va a multiplicar por el pulso de altura 3 y luego se van a sumar las multiplicaciones:
(1\cdot 3) + (1 \cdot 2) = 3 + 2 = 5
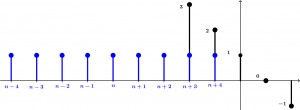
Y así sucesivamente vamos a ir moviendo la señal h[n] hasta que haya recorrido toda la señal x[n]. Vamos a ver todas las operaciones:
\begin{array}{l c l c l c c}
n < -6 & = & & & & & 0 \\
n = -6 & = & (3 \cdot 1) & = & 3 & = & 3 \\
n = -5 & = & (3 \cdot 1) + (2 \cdot 1) & = & 3 + 2 & = & 5 \\
n = -4 & = & (3 \cdot 1) + (2 \cdot 1) + (1\cdot 1) & = & 3 + 2 + 1 & = & 6 \\
n = -3 & = & (3 \cdot 1) + (2 \cdot 1) + (1\cdot 1) + (0 \cdot 1) & = & 3 + 2 + 1 + 0 & = & 6 \\
n = -2 & = & (3 \cdot 1) + (2 \cdot 1) + (1\cdot 1) + (0 \cdot 1) + (-1 \cdot 1) & = & 3 + 2 + 1 + 0 \ - 1 & = & 5 \\
n = -1 & = & (3 \cdot 1) + (2 \cdot 1) + (1\cdot 1) + (0 \cdot 1) + (-1 \cdot 1) & = & 3 + 2 + 1 + 0 \ - 1 & = & 5 \\
n = 0 & = & (3 \cdot 1) + (2 \cdot 1) + (1\cdot 1) + (0 \cdot 1) + (-1 \cdot 1) & = & 3 + 2 + 1 + 0 \ - 1 & = & 5 \\
n = 1 & = & (3 \cdot 1) + (2 \cdot 1) + (1\cdot 1) + (0 \cdot 1) + (-1 \cdot 1) & = & 3 + 2 + 1 + 0 \ - 1 & = & 5 \\
n = 2 & = & (3 \cdot 1) + (2 \cdot 1) + (1\cdot 1) + (0 \cdot 1) + (-1 \cdot 1) & = & 3 + 2 + 1 + 0 \ - 1 & = & 5 \\
n = 3 & = & (2 \cdot 1) + (1\cdot 1) + (0 \cdot 1) + (-1 \cdot 1) & = & 2 + 1 + 0 \ - 1 & = & 2 \\
n = 4 & = & (1\cdot 1) + (0 \cdot 1) + (-1 \cdot 1) & = & 1 + 0 \ - 1 & = & 0 \\
n = 5 & = & (0 \cdot 1) + (-1 \cdot 1) & = & 0 \ - 1 & = & -1 \\
n = 6 & = & (-1 \cdot 1) & = & - 1 & = & -1 \\
n > 6 & = & & & & & 0
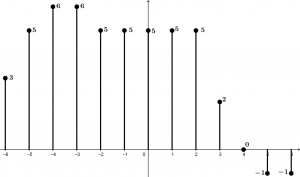
\end{array}Finalmente la gráfica de la convolución se verá de la siguiente manera:
¡Y eso es todo!
Te adjunto un PDF con toda la explicación del artículo, disfrútalo ;)
RBJLabs-Convolución_Caso_Continuo_Análogo
Gracias por estar en este momento con nosotros : )