Entre tantos teoremas de probabilidad, aquí presentamos uno que muchos hemos escuchado, el muy conocido Teorema de Bayes. Por eso te hemos traído una explicación y un ejemplo para ilustrar la explicación.
Vamos con la explicación del Teorema de Bayes
Tenemos varios eventos que son A_{1},A_{2},A_{3},..,A_{k},..,A_{n}, que forman una partición con S, y E es un evento cualquiera. Si aplicamos lo antes visto en la fórmula de probabilidad condicional:
P(A_{k}|E) = \cfrac{P(A_{k}\cap E)}{P(E)} = \cfrac{P(A_{k})P(E|A_{k})}{P(E)}
La parte P(A_{k}|E) de la fórmula anterior se lee:
La probabilidad de que haya sido A_{k} dado que ya sucedió E
Fórmula del Teorema de Bayes
Si consideramos la fórmula anterior obtenida para calcular la probabilidad total de E, se tiene que aplicar la sumatoria que se muestra a continuación para calcular la probabilidad total de E ya que se tienen varios casos en los ejercicios que requieren el uso de esta fórmula, lo que se muestra a continuación es la Fórmula del Teorema de Bayes:
\displaystyle P(A_{k}|E) = \cfrac{P(A_{k})P(E|A_{k})}{\sum_{i=1}^{n}P(A_{i})P(E|A_{i})}
La sumatoria del denominador se lee así:
La suma de la probabilidad de A_{i} multiplicado por la probabilidad de que sea E dado que ya ocurrió A_{i}.
Teorema de Bayes, ejercicio
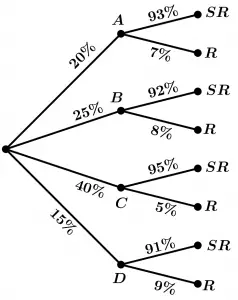
La compañía X usa cuatro empresas de transporte: A_{1}, A_{2}, A_{3} y A_{4}. Se sabe que 20% de los embarques se asignan a la empresa A_{1}, 25% a la A_{2}, 40% a la A_{3} y 15% a la A_{4}. Los embarques llegan retrasados a sus clientes en 7% si los entrega A_{1}, 8%si es A_{2}, 5% si es A_{3} y 9% si es A_{4}. Si sabemos que el embarque de hoy fue entregado con retraso, ¿cuál es la probabilidad de que haya sido la empresa A_{1} la encargada de hacerlo?
Muchas personas de ustedes ya sabrán rápidamente cómo resolver este ejercicio, pero vamos a explicarlo paso a pasito. Vamos a representar la información en la siguiente tabla:
\begin{array}{| c | c |}
\hline
\text{Embarques} & \text{Entrega} \\
\hline
A_{1} = 20 \% & \text{Retraso (R)} = 7\% \\
A_{2} = 25\% & \text{Retraso (R)} = 8\% \\
A_{3} = 40\% & \text{Retraso (R)} = 5\% \\
A_{4} = 15\% & \text{Retraso (R)} = 9\% \\
\hline
\end{array}R = \text{Retraso} SR = \text{Sin Retraso}
El equipo de logística nos está informando desde la cabina que llegó un encargo y se retrasó, y como lo que queremos saber es si fue la empresa A_{1}, en otras palabras, saber si fue A_{1} debido a que ya se retrasó, entonces utilizaremos la fórmula del teorema de Bayes:
\displaystyle P(A_{1}|R) = \cfrac{P(A_{1})P(R|A_{1})}{\sum_{i=1}^{4}P(A_{i})P(R|A_{i})}
n es igual a 4 porque vamos a representar la probabilidad del retraso de las 4 empresas. Vamos a hallarla:
\displaystyle \sum_{i=1}^{4}P(A_{i})P(R|A_{i}) = P(A_{1})P(R|A_{1}) + P(A_{2})P(R|A_{2}) + P(A_{3})P(R|A_{3}) + P(A_{4})P(R|A_{4})
Con la tabla escrita, es más fácil colocar los valores, mira la sumatoria con los valores de la tabla:
\displaystyle \sum_{i=1}^{4}P(A_{i})P(R|A_{i}) = (20\%)(7\%) + (25\%)(8\%) + (40\%)(5\%) + (15\%)(9\%)
Puedes agarrar una calculadora para agilizar el proceso de multiplicar y sumar:
\displaystyle P = (E) = \sum_{i=1}^{4}P(A_{i})P(R|A_{i}) = \cfrac{7}{500} + \cfrac{1}{50} + \cfrac{1}{50} + \cfrac{27}{2000} = \cfrac{27}{400}
Sólo falta calcular la probabilidad del numerador de la fórmula del Teorema de Bayes, la cual tiene P(A_{1}) que es 20\% y tiene P\left( \frac{E}{A_{1}} \right) que es la probabilidad de que haya llegado con retraso si ya ocurrió que llegó en el embarque A_{1} que tiene una probabilidad de 7\%. Ahora sí, sustituyamos todos estos valores en la fórmula del Teorema de Bayes:
P(A_{1}|E) = \cfrac{\cfrac{20}{100} \cdot \cfrac{7}{100}}{\cfrac{27}{400}} = \cfrac{28}{135}=0.2074
Así que la probabilidad de que llegue una embarcación con retraso y además venga de la embarcación A es de 0.2074 que es igual al 20.74\%
Gracias por estar en este momento con nosotros : )