Este ejercicio nos lo comentó Clara, una de nuestras lectoras que le agradecemos mucho el ejercicio que nos escribió.
Dice así:
Suponiendo que el conjunto universo son los números naturales, si un conjunto A son los números pares entre 2 y 100 y el conjunto B son los múltiplos de 3 entre 3 y 100, ¿cómo represento el resto de los números en el rectángulo si ésta es una cantidad infinita de ellos? ¿Cómo se representa un conjunto infinito en los Diagramas de Venn?
Realizamos un Diagrama de Venn donde se muestran todos los números del 2 al 100, el cual es el que puedes apreciar a continuación:
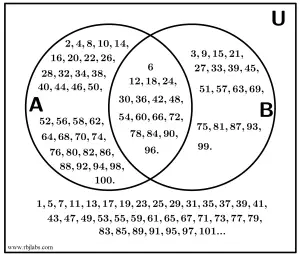
Esa es la forma de representarlo gráficamente, pero para representarlo en la forma escrita necesitamos definir primero nuestro conjuntos A y B, los cuáles se representan de la siguiente manera:
A = \{ x \in N / x = 2n, \ n \in N\}
B = \{ x \in N / x = 3n, \ n \in N\}
En el conjunto A se escribió que x pertenece a los números reales N, pero el conjunto A tiene que x son los números pares, así que simplemente es que x = 2n.
En el conjunto B se escribió que x pertenece a los números reales N, pero el conjunto B tiene que x son los números múltiplos de 3 entre el 3 y 100, así que simplemente es que x = 3n.
Ahora, para redactar el complemente y los números que no son ni el conjunto A ni el B, lo podemos escribir de la siguiente forma:
C = \{ x \in N / x = (A \cup B)^{c} \}
Donde A\cup B es la unión de los conjuntos A y B y la c que está como exponente es el complemento. Así que esa expresión se lee: “Complemento de unión A y B“.
Esperamos te haya sido de ayuda y que haya quedado claro.
Gracias por estar en este momento con nosotros : )
