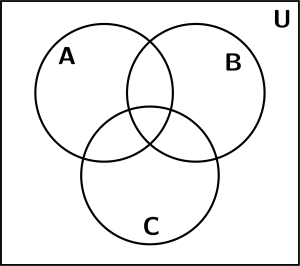
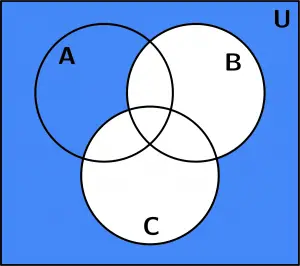
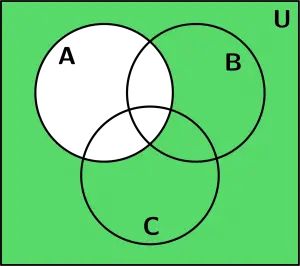
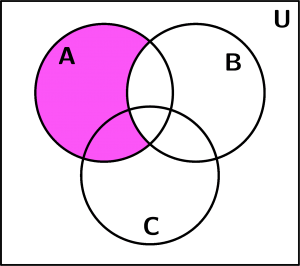
Vamos a ver 3 ejemplos de conjuntos con Diagramas de Venn. Utilizaremos ejemplos de 3 conjuntos, el conjunto A, el conjunto B y el conjunto C y nuestra figura base con la que representaremos los ejemplos de conjuntos con diagramas de venn es la siguiente:
Primer ejemplo de conjuntos con Diagramas de Venn
Nuestro primer ejemplo de conjuntos es: A \cap (B \cup C)^{\text{C}}
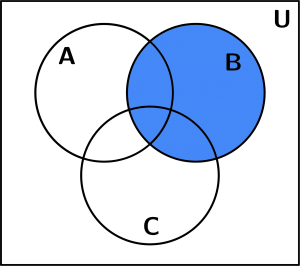
Vamos a comenzar con los paréntesis, tomaremos B y representaremos gráficamente cómo se vería en un diagrama de Venn:
Conjunto B
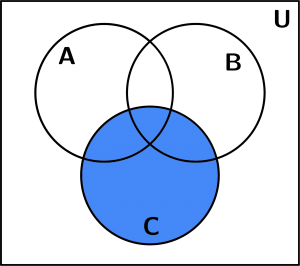
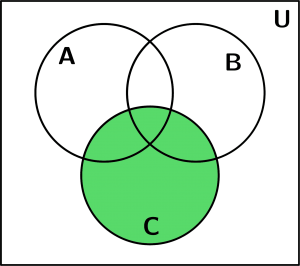
Representamos gráficamente C:
Conjunto C
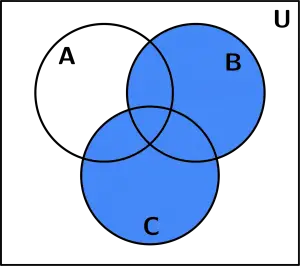
Realizamos la unión de B con C. (B \cup C):
(B \cup C)
Seguidamente se efectuó el complemento que tiene el paréntesis. (B \cup C)^{\text{C}}
(B \cup C)^{\text{C}}
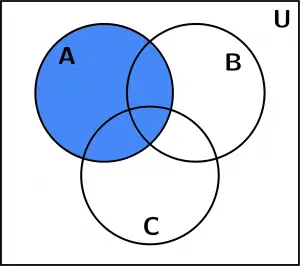
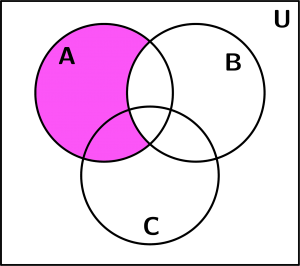
Después graficaremos el área que ocupa sólo el conjunto A para tenerlo más visualmente:
Conjunto A
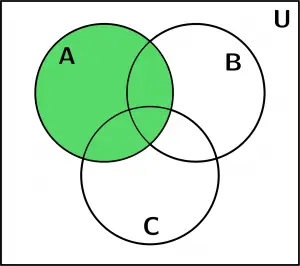
Finalmente se realizó la intersección que se indica en el ejemplo, así que la respuesta es:
A \cap (B \cup C)^{\text{C}}
Segundo ejemplo de Diagramas de Venn
Nuestro segundo ejemplo es: C \cup (A^{\text{C}} \cap A)
Ahora, como hicimos en el ejemplo anterior, empezaremos con lo que está dentro de los paréntesis, identificando cada área que dice el enunciado del ejemplo.
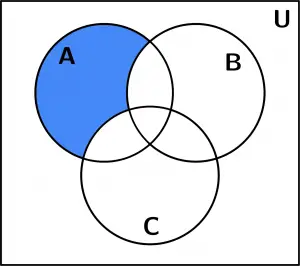
Colocamos gráficamente el conjunto A:
Conjunto A
El complemento de A se vería de la siguiente manera:
Complemento de A: A^{\text{C}}
Después se efectuó la intersección (A^{\text{C}} \cap A):
(A^{\text{C}} \cap A)
Seguidamente se dibujó el conjunto C:
Conjunto C
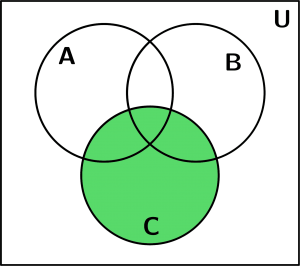
Y finalmente para llegar al resultado, se realizó la unión de C con (A^{\text{C}} \cap A), el cual se observó que el resultado es el mismo conjunto de C:
C \cup (A^{\text{C}} \cap A)
Tercer ejemplo con Diagramas de Venn
El tercer ejemplo de conjuntos con Diagramas de Venn es: (A - B) \cap (C \cup B^{\text{C}})
Comenzando con la resolución del ejercicio, primero se dibujaron los conjuntos A y B:
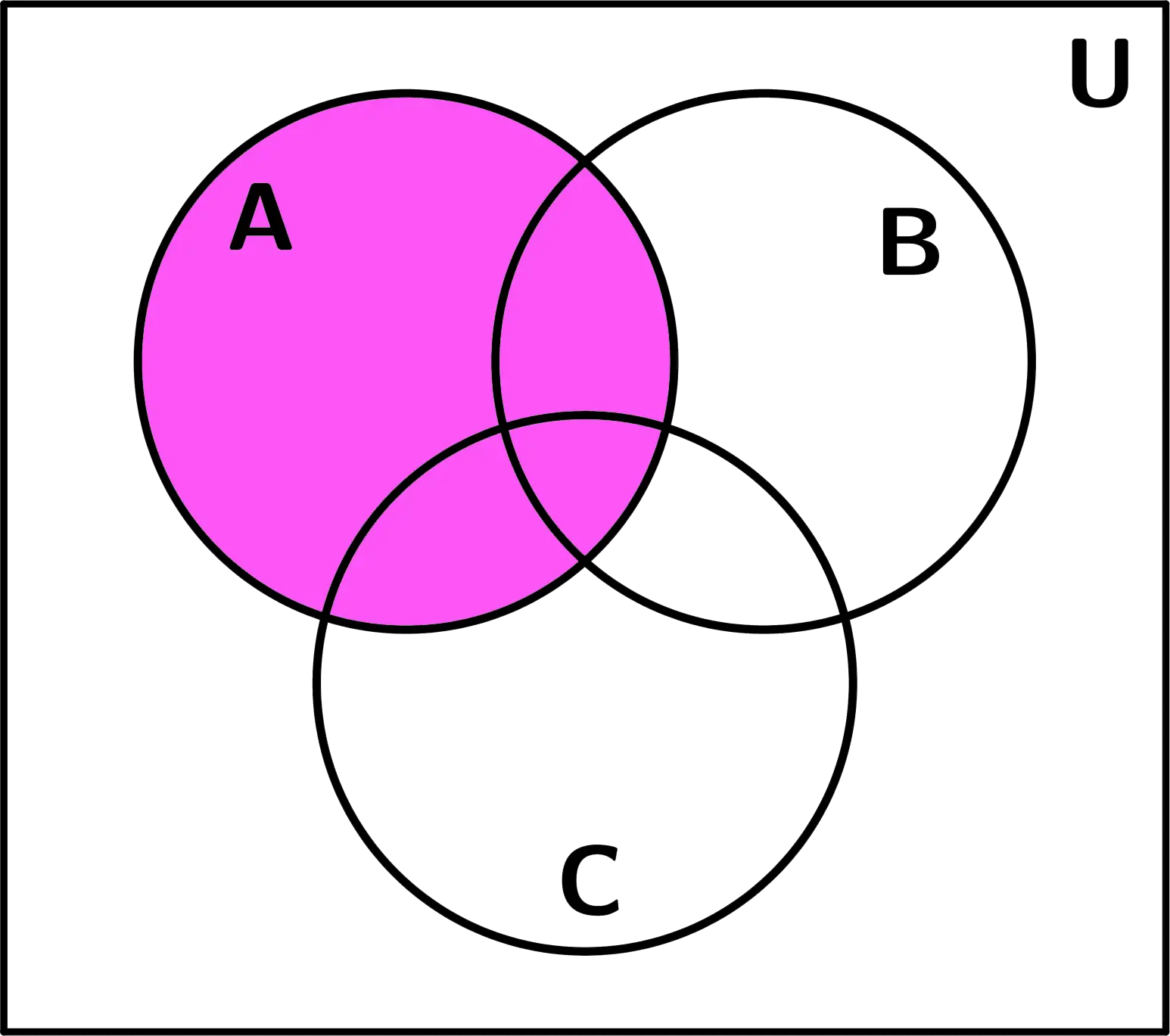
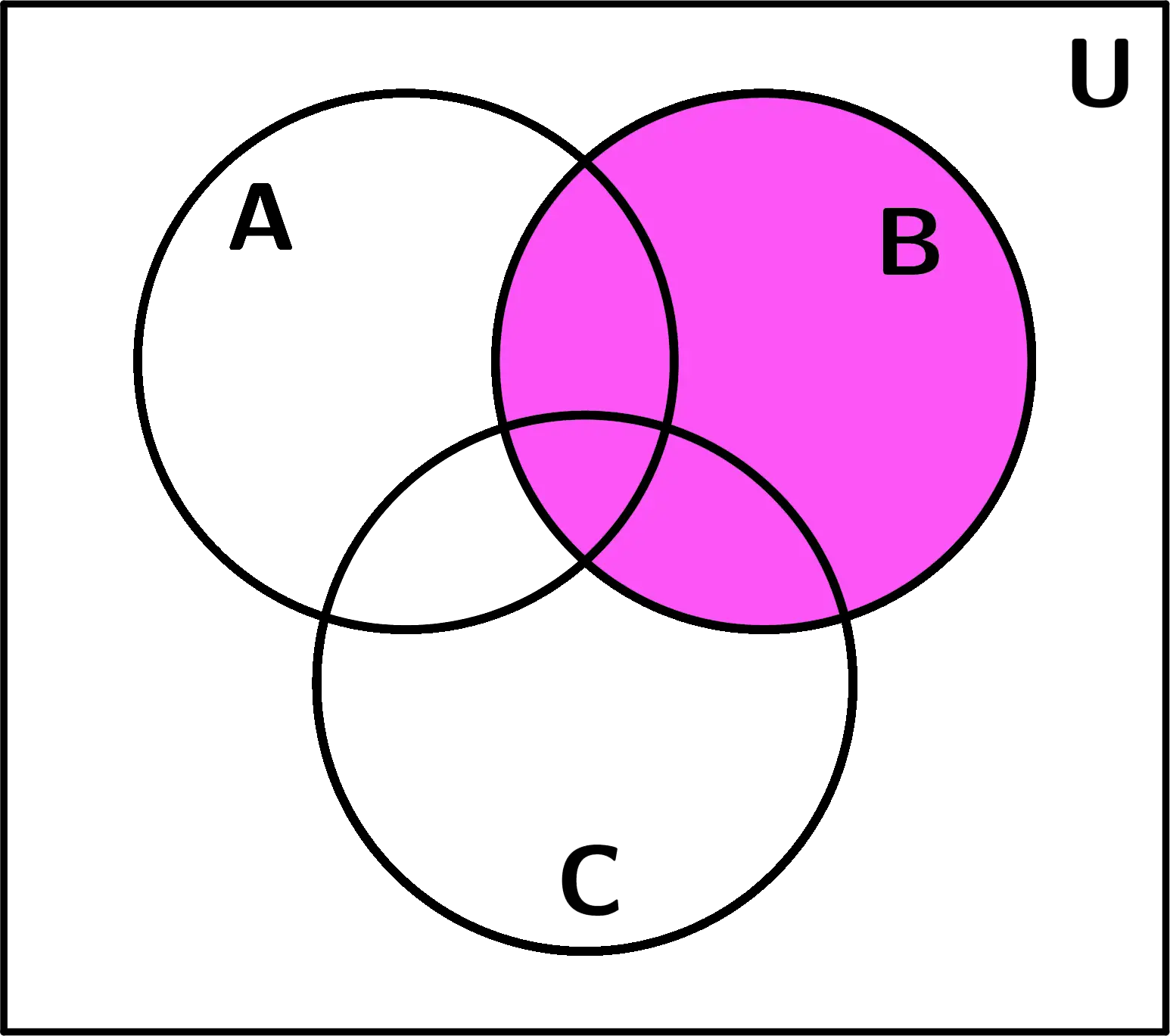
Y seguidamente se realizó la diferencia A - B:
A - B
Después se procedió a realizar el interior del otro paréntesis, primero dibujando el conjunto C y luego el complemento del conjunto B:
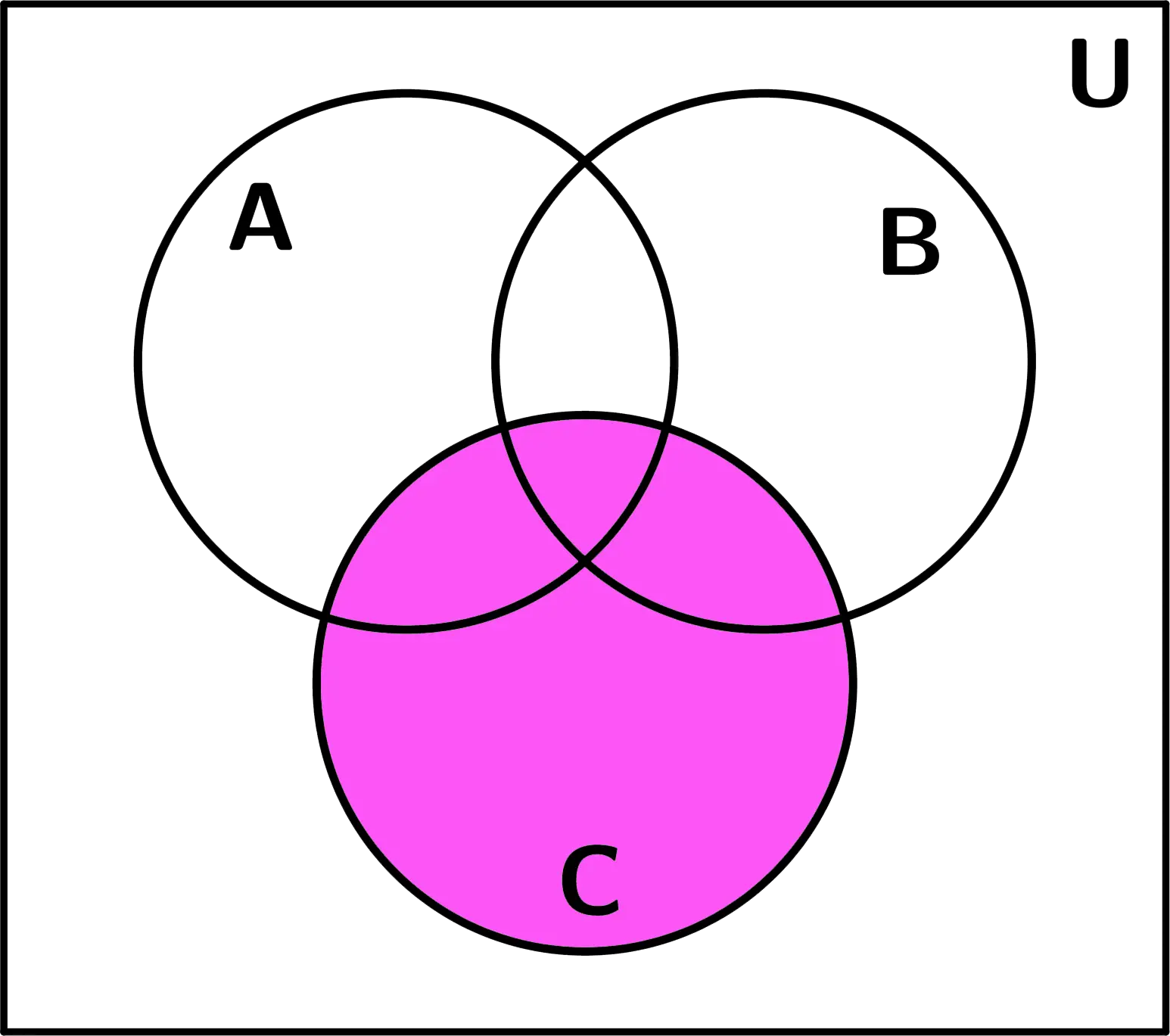
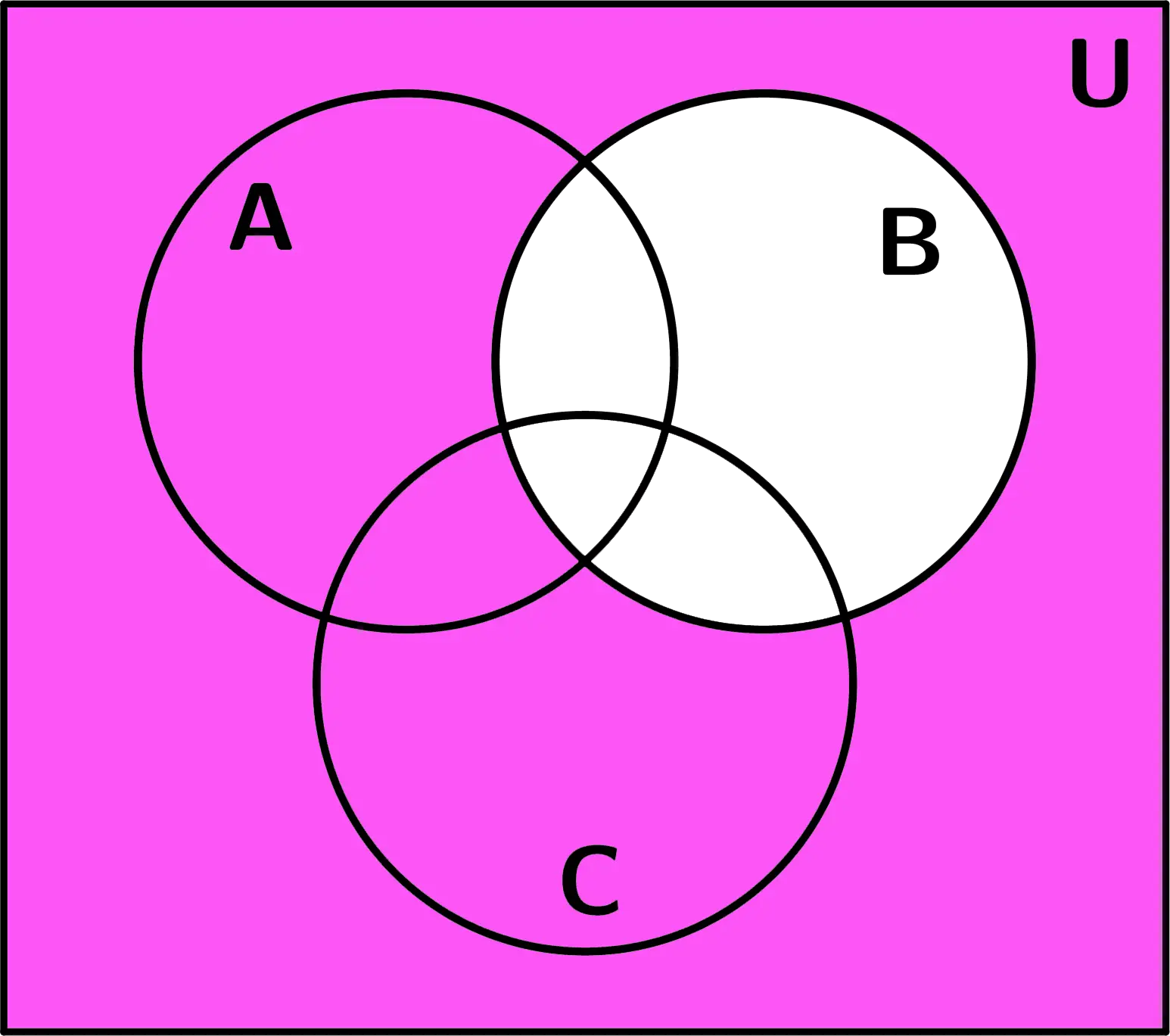
Finalmente para llegar al resultado se efectuó la intersección que dice el ejemplo, el resultado sería:
(A - B) \cap (C \cup B^{\text{C}})
Gracias por estar en este momento con nosotros : )