Sencilla explicación de lo que es el diagrama de Venn. Operaciones básicas de los conjuntos representadas con diagramas de Venn ¡Ejemplos con diagramas de Venn y finalmente veremos fórmulas de conteo importantes! Ya se manejan unas pizarras muy geniales para realizar de una manera más práctica y visible este tipo de ejercicios.
¿Qué es un Diagrama de Venn?
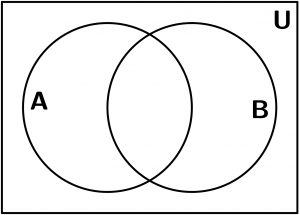
Simple, es la representación gráfica de los conjuntos.
A y B son conjuntos cualquiera
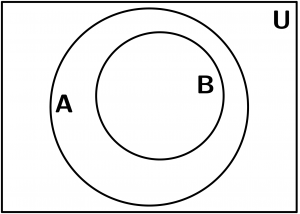
B es un subconjunto de A
Operaciones básicas de los conjuntos
Unión en los diagramas de venn (\cup)
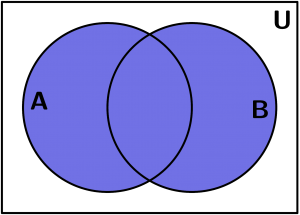
Es el conjunto de todos los elementos que pertenecen a A o B. Es decir:
A \cup B = \{ x:x \in A\lor x \in B\}
A \cup B
Intersección en los diagramas de venn (\cap)
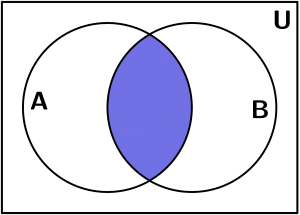
Es el conjunto de los elementos que pertenecen a A y B. Quiere decir que sólo se queda dibujada la parte que comparten los conjuntos:
A \cap B = \{ x:x \in A \land x \in B\}
A \cap B
Complemento de un conjunto (^{\text{C}})
Es el conjunto de elementos que pertenecen al universo que no forma parte de A. Dicho de otra forma:
A^{\text{C}} = \{ x:x\in U, x \notin A\}
A^{\text{C}}
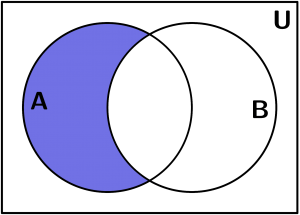
Diferencia en los diagramas de venn (-)
Es el conjunto que se genera al quitar los elementos presentes en el segundo conjunto:
A- B = \{ x:x \in A, x \notin B\}
A- B
Ejemplo de conjuntos con Diagramas de Venn
Supón que el Universo está definido de la siguiente forma:
U = \{ 1,2,3,4,5,6,7,8,9,10\}
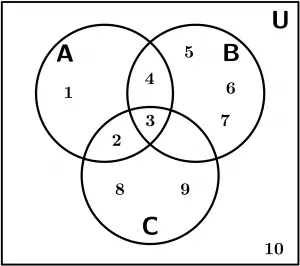
Y se delimitan los siguientes conjuntos:
A = \{ 1,2,3,4\}, \ B = \{ 3,4,5,6,7\}, \ C = \{ 2,3, 8,9\}
El diagrama de Venn queda representado de la siguiente forma:
Perfecto, empecemos con los ejemplos de Diagramas de Venn
Primer Ejemplo de diagrama de venn
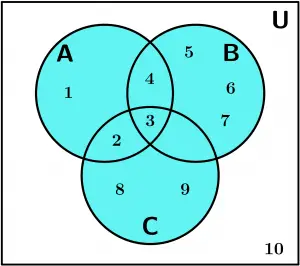
Realiza la unión del conjunto A con el conjunto B y la unión del conjunto B con el conjunto C:
A \cup B \cup C
Realizando lo anterior, los números que tendríamos son los siguientes:
\{ 1,2,3,4,5,6,7,8,9\}
A \cup B \cup C
Segundo Ejemplo de diagrama de venn
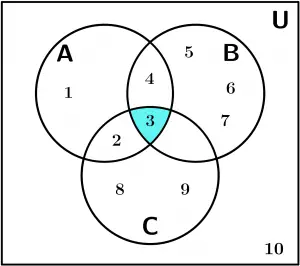
Realiza la intersección del conjunto A con el conjunto B y la intersección del conjunto B con el conjunto C:
A \cap B \cap C
Realizando lo anterior, el número que nos queda es sólo uno ya que es lo que los tres conjuntos tienen en común:
\{ 3\}
A \cap B \cap C
Tercer Ejemplo de diagrama de venn
Realiza el complemento del conjunto A menos la intersección del conjunto B con el conjunto C:
A^{\text{C}} - (B \cap C)
Es importante hacer los pasos en orden:
- Se priorizan los paréntesis, así que primero se realiza B \cap C:
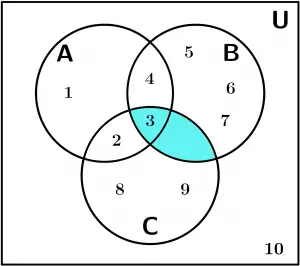
B \cap C
2. Seguidamente se visualiza el complemento de A:
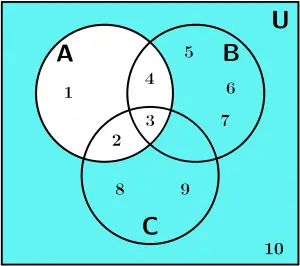
A^{\text{C}}
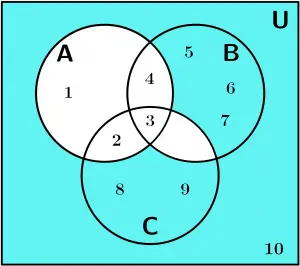
3. Finalmente se realiza la diferencia A^{\text{C}} - (B \cap C)
A^{\text{C}} - (B \cap C)
Resultado:
\{ 5,6,7,8,9,10\}
Fórmulas de conteo de diagramas de venn
Si n(A), n(B) y n(C) son el número de elementos que conforman a los conjuntos A, B y C respectivamente, entonces las fórmulas de diagramas de venn son:
- n(A \cup B) = n(A) + n(B) - n(A \cap B)
- n(A - B)=n(A) - n(A \cap B)
- n(A^{\text{C}}) = n(U) - n(A)
- n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(A \cap C) - n(B \cap C) + n(A \cap B \cap C)
Gracias por estar en este momento con nosotros : )