Definición de intervalo
Se le llama intervalo al subconjunto de números reales comprendidos entre dos cualesquiera de sus elementos: a y b ; a los cuales se le denominan extremos del intervalo.
Geométricamente, los intervalos corresponden a segmentos de recta, semirrectas o a la misma recta real.
Intervalo cerrado
Es el conjunto de números reales formados por a , b y todos los elementos comprendidos entre ambos. Es decir, es aquel intervalo cuyos extremos pertenecen al intervalo dado y se representa a través de corchetes [ ] .
[a,b] = \{ x / a \le x \le b \}
Con respecto a la notación gráfica, se denota mediante círculos rellenados, denotados como cerrado. Es decir, como se muestra en la imagen siguiente:

Intervalo abierto
Es el conjunto de los números reales comprendidos entre a y b . Es decir, es aquel intervalo cuyos extremos no están contenidos en el intervalo, sólo sirven de fronteras. Para representar este intervalo, se emplean paréntesis ( ) .
(a,b) = \{ x / a < x < b \}
Con respecto a la notación gráfica, se denota mediante círculos vacíos, denotados como abiertos. Es decir, como se muestra en la siguiente gráfica:

Intervalo semiabierto o semicerrado
Es aquel intervalo que no contiene a uno de los extremos, éste puede estar situado a la derecha o izquierda. Se representa combinando paréntesis y corchetes: ( ] o [ ) . Es decir:
Intervalo semiabierto a izquierda (o semicerrado a derecha)
(a,b] = \{ x / a < x \le b \}

Intervalo semiabierto a derecha (o semicerrado a izquierda)
[a,b) = \{ x / a \le x < b \}

Intervalo infinito
Es aquel intervalo que tiene al menos uno de sus extremos al infinito \infty . El infinito al ser una cantidad inconmensurable (no medible) emplea paréntesis para su representación.
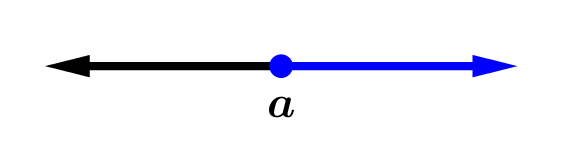 | 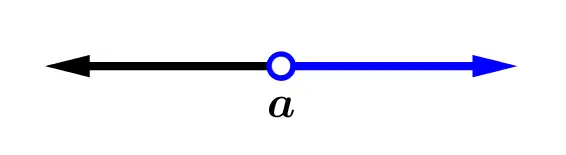 |
| [a,+\infty) = {x / x \ge a } | (a,+\infty)={ x / x > a } |
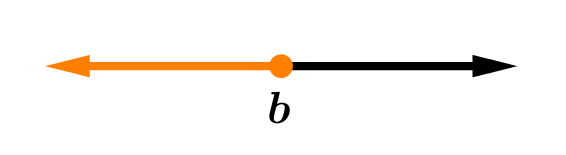 | 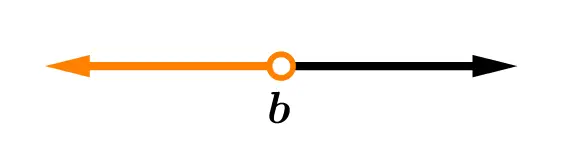 |
| (-\infty, b] = { x / x \le b } | (-\infty,b) = {x / x < b } |
| (-\infty,+\infty) = \mathbb{R} |  |
Gracias por estar en este momento con nosotros : )
