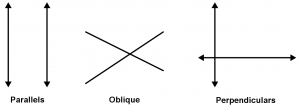
Definition of parallel lines
Two lines are parallel and do not intersect for longer than they are prolonged.
Properties of parallel lines
The 3 properties that parallel lines have are the following:
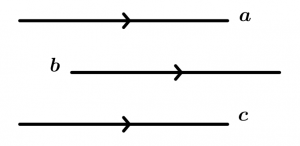
They are symmetric or reciprocal
This property says that if a line a is parallel to a line b, then the line b is parallel to the line a.
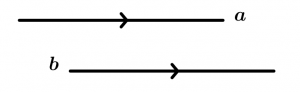\text{If } \ a \parallel b \ \text{ then } b \parallel a
They are transitive
If a line a is parallel to a line b and the line b is parallel to a line c, then the line c is parallel to the line a.
\text{If } \ a \parallel b \ \text{ and } \ b \parallel c \ \text{ then } \ c \parallel a
Identical or reflective
This property tells us that every line is parallel to itself.
a \parallel a
Postulates of parallel lines
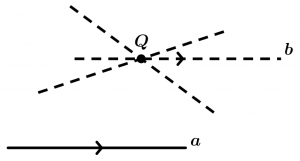
Postulate of Euclid (of the parallels)
For a point Q out of a line a passes one and only one parallel to said line.
This postulate means that only one parallel line will pass through the point Q, no more than two parallel lines can pass at the point Q.
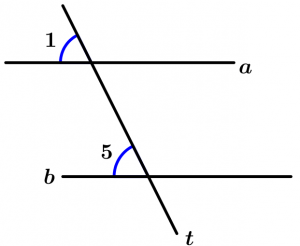
Postulate of lines cut by a transversal
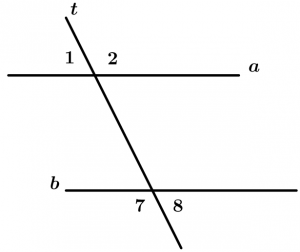
If two lines a and b are cut by a transversal line t and a pair of corresponding angles are congruent, then the lines a and b are parallel.
\text{If } \ \measuredangle 1 \cong \measuredangle 5
\text{then} \ a \parallel b
Theorems of parallel lines
Theorem 1
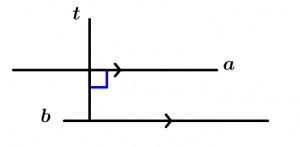
If two lines a and b are perpendicular to a line t, then a and b are parallel.
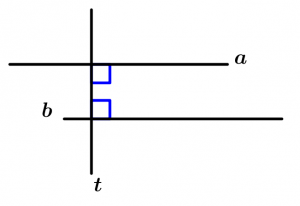\text{If } \ a \bot t \ \text{ and } \ b \bot t
\text{then } \ a \parallel b
Theorem 2
If one line t cuts another, it also cuts to any parallel to it.
Theorem 3
Any perpendicular to a line, is perpendicular to any parallel to it.
\text{If } \ a \parallel b \ \text{ and } \ a \bot t
\text{then } \ b \bot t
Before continuing with the theorems
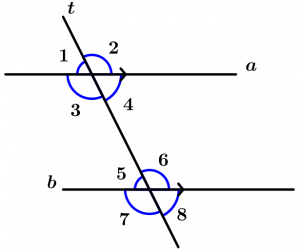
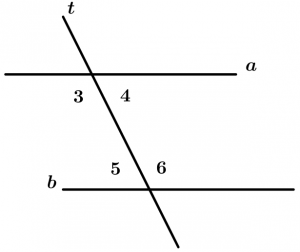
Before continuing with the theorems, we have to make clear some concepts, they are simple but necessary. We will see the internal angles, the external angles, corresponding angles, alternate interior angles, internal conjugate angles and the conjugate external angles. Let’s go to the examples.
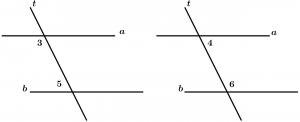
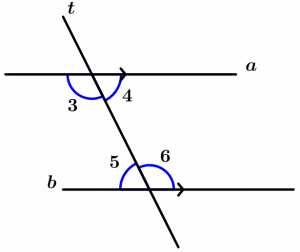
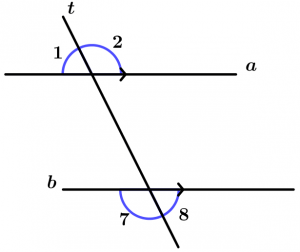
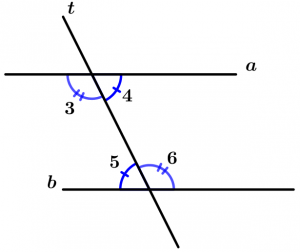
Internal angles
Are those angles that are between the two lines that are cut by the transversal, these angles are 3, 4, 5 and 6.
\measuredangle 3, \measuredangle 4, \measuredangle 5 \ \text{ and } \ \measuredangle 6
\text{are internal angles}
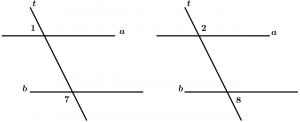
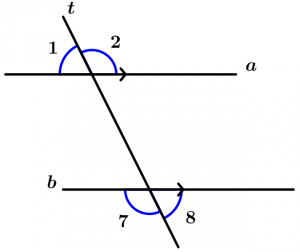
External angles
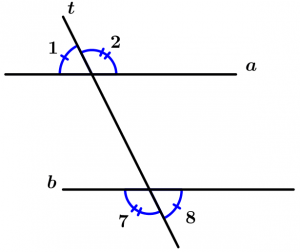
Are those angles that are not between the two lines and are cut by the transversal, these angles are 1, 2, 7 and 8.
\measuredangle 1, \measuredangle 2, \measuredangle 7 \ \text{ and } \measuredangle 8
\text{are external angles}
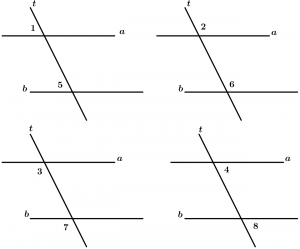
Corresponding angles
Are all those angles that are located on the same side of the transversal, one is internal and the other is external, are grouped by pairs which are 4.
The corresponding pairs of angles are:
\text{Pair 1: } \ \measuredangle 1 \text{ and }\measuredangle 5
\text{Pair 2: } \ \measuredangle 2 \text{ and }\measuredangle 6
\text{Pair 3: } \ \measuredangle 3 \text{ and }\measuredangle 7
\text{Pair 4: } \ \measuredangle 4 \text{ and }\measuredangle 8
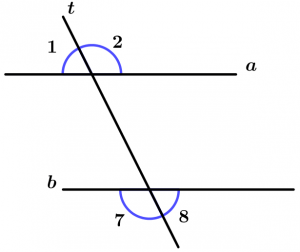
Internal alternate angles
They are two internal angles with different vertex and they are on different sides of the transversal, they are grouped by pairs and there are 2.
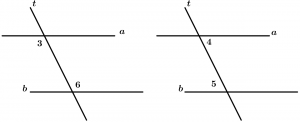Pairs of internal alternate angles:
\text{Pair 1: } \ \measuredangle 3 \text{ and }\measuredangle 6
\text{Pair 2: } \ \measuredangle 4 \text{ and }\measuredangle 5
Alternate external angles
They are two external angles with different vertex and that are on different sides of the transversal, are grouped by pairs and are 2.
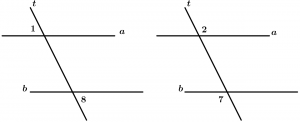Pairs of external alternate angles:
\text{Pair 1: } \ \measuredangle 1 \text{ and }\measuredangle 8
\text{Pair 2: } \ \measuredangle 2 \text{ and }\measuredangle 7
Internal conjugated angles
They are two internal angles with different vertex and that are on the same side of the transversal, are grouped by pairs and are 2.
Pairs of internal conjugated angles:
\text{Pair 1: } \ \measuredangle 3 \text{ and }\measuredangle 5
\text{Pair 2: } \ \measuredangle 4 \text{ and }\measuredangle 6
External conjugated angles
They are two external angles with different vertex and that are on the same side of the transversal, are grouped by pairs and are 2.
Pairs of external conjugated angles:
\text{Pair 1: } \ \measuredangle 1 \text{ and }\measuredangle 7
\text{Pair 2: } \ \measuredangle 2 \text{ and }\measuredangle 8
Theorem 4
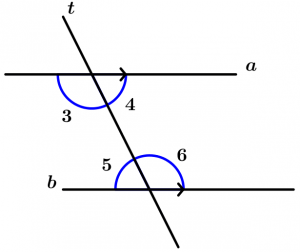
If a line a and b are cut by a transversal line t and it turns out that a pair of alternate internal angles are congruent, then the lines a and b are parallel.
\text{If a statement says that } \ \measuredangle 3 \cong \measuredangle 6
\text{or what } \ \measuredangle 4 \cong \measuredangle 5
\text{then } \ a\parallel b
Theorem 5. The PAI theorem
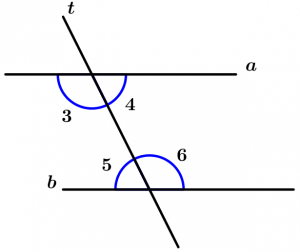
If two parallel lines a and b are cut by a transversal line t, then the alternate internal angles are congruent.
\text{If } \ t \ \text{ cut to parallel } a \ \text{ and } \ b
\text{then } \ \measuredangle 3\cong \measuredangle 6 \ \text{ and } \ \measuredangle 4 \cong \measuredangle 5
Theorem 6
Any transversal line t forms with two parallel lines a and b, alternating external angles congruent.
Theorem 7
Theorem 8
Any transversal line t forms with two parallel lines a and b corresponding angles congruent.
Pairs of corresponding congruent angles:
\text{Pair 1: } \ \measuredangle 1 \text{ and }\measuredangle 5
\text{Pair 2: } \ \measuredangle 2 \text{ and }\measuredangle 6
\text{Pair 3: } \ \measuredangle 3 \text{ and }\measuredangle 7
\text{Pair 4: } \ \measuredangle 4 \text{ and }\measuredangle 8
Theorem 9
If two parallel lines a and b are cut by a transversal line t, then the internal conjugate angles are supplementary.
\text{If the parallel lines} \ a \ \text{ and } \ b
\text{are cut by } \ t, \ \text{ then}
\measuredangle 3 + \measuredangle 5 = 180^{\text{o}}
\measuredangle 4 + \measuredangle 6 = 180^{\text{o}}
Theorem 10
If two lines a and b are cut by a transversal line t and the internal conjugate angles are supplementary, then the lines a and b are parallel.
\text{If the lines } \ a \ \text{ and } \ b \ \text{are cut by }
t \ \text{ and the statement says that:}
\measuredangle 3 + \measuredangle 5 = 180^{\text{o}} \ \text{ or what}
\measuredangle 4 + \measuredangle 6 = 180^{\text{o}}
\text{then} \ a \parallel b
Theorem 11
If two parallel lines a and b are cut by a transversal line t, then the external conjugate angles are supplementary.
\text{If the parallel lines} \ a \ \text{ and } \ b
\text{are cut by } \ t, \ \text{ then}
\measuredangle 1 + \measuredangle 7 = 180^{\text{o}} \ \text{ and}
\measuredangle 2 + \measuredangle 8 = 180^{\text{o}}
Theorem 12
If two lines a and b are cut by a transversal line t and the conjugated external angles are supplementary, the lines a and b are parallel.
\text{If the lines } \ a \ \text{ and } \ b \ \text{are cut by }
t \ \text{ and the statement says that:}
\measuredangle 1 + \measuredangle 7 = 180^{\text{o}} \ \text{ or what}
\measuredangle 2 + \measuredangle 8 = 180^{\text{o}}
\text{then } \ a \parallel b
Theorem 13
If two angles have their sides respectively parallel, these angles are congruent or supplementary.
\measuredangle 1 \cong \measuredangle 2
\measuredangle 3 + \measuredangle 4 = 180^{\text{o}}
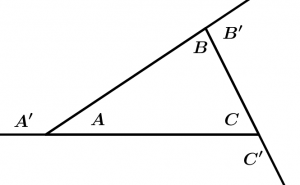
Theorem 14, 15, 16
14. The sum of the measures of the internal angles of a triangle is equal to 180 °.
\measuredangle A + \measuredangle B + \measuredangle C = 180^{\text{o}}
15. The sum of the measurements of the outer angles of a triangle is equal to 360 °.
\measuredangle A' + \measuredangle B' + \measuredangle C' = 360^{\text{o}}
16. The measure of any exterior angle of a triangle is equal to the sum of the measurements of the two non-adjacent interior angles.
\measuredangle A' = \measuredangle B + \measuredangle C
\measuredangle B' = \measuredangle A + \measuredangle C
\measuredangle C' = \measuredangle A + \measuredangle B
Thank you for being at this moment with us : )
