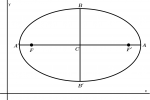
Ellipse with center at C(x_{0}, y_{0}) and with a major axis parallel to the axis x
Let’s look at our base figure of the ellipse with which we will define the formulas of the ellipse:
Equation of the ellipse in rectangular coordinates:
The equation of the ellipse is very similar to the equation of the hyperbola, the only difference is that the negative sign that appears between the fractions of the hyperbola, is now positive, which results in an ellipse, our equation of the ellipse is:
\cfrac{(x - x_{0})^{2}}{a^{2}} + \cfrac{(y - y_{0})^{2}}{b^{2}} = 1
Which x_{0} and y_{0} represent the center of the ellipse located in the Cartesian plane.
a represents half the length of the major axis
b represents half the length of the minor axis
Length of the major axis of the ellipse
The length of the ellipse’s major axis is \overline{A'A} = 2a
Where a is the distance from the center C to A or A'
Length of the minor axis of the ellipse
The length of the minor axis of the ellipse is \overline{B'B} = 2b
Where b is the distance from the center C to B or B'
Ellipse Area
The area of the ellipse is calculated using the following formula:
A = \pi \cdot a \cdot b
In which:
a is half the length of the major axis
b is half the length of the minor axis
Distance from the center to the focus (c)
The length of the center C to the focus F or F' is:
c = \sqrt{a^{2} \ - b^{2}}
Eccentricity of the ellipse
The formula for calculating the eccentricity of the ellipse is as follows:
\epsilon = \cfrac{c}{a} = \cfrac{\sqrt{a^{2} - b^{2}}}{a}
The eccentricity can only take values between 0 and 1 \ \rightarrow \ 0< \epsilon <1, but now:
What does eccentricity mean in the ellipse or what does it represent?
The eccentricity represents how elongated an ellipse is, it means that as long as an ellipse has an eccentricity close to the value of 1, it will be longer, if the eccentricity equals 1, there would be no ellipse, it would be a straight line! As long as the eccentricity value has a value closer to zero, it will resemble a circle.
If you calculate the eccentricity of an “ellipse” and is equal to zero, it is a circumference!
Example of an ellipse with center C(x_{0}, y_{0}) and with a major axis parallel to the axis x
The equation of the ellipse is:
\cfrac{(x - 6)^{2}}{5^{2}} + \cfrac{(y - 4)^{2}}{3^{2}} = 1
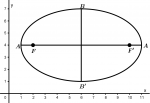
The center of the ellipse
As you can see, the center C of the ellipse is located at the point:
C(6,4)
That means that the center of our ellipse will be in the values that have x_{0} and y_{0} only that we will place the opposite signs in our coordinate, that means that as our value of x_{0} is -6 and our value of y_{0} is -4, so our coordinate of the center of the ellipse will be C(6, 4).
Length of the major axis of the ellipse
The length of the major axis \overline{A'A} is equal to 10, which means that the length of a which is the length of \overline{CA} or \overline{CA'} is equal to 5.
Length of the minor axis of the ellipse
The length of the minor axis \overline{B'B} is equal to 6, which means that the length of b which is the length of \overline{CB} or \overline{CB'} is equal to 3.
Distance from the center to the focus of the ellipse
The distance from the center C to either of the focus, F or F' is:
c = \sqrt{5^{2} - 3^{2}} = \sqrt{25 - 9} = \sqrt{16} = 4
Which means that the focus F is at the point F(2, 4) and the focus F' is at the point F'(10, 4)
Ellipse Area
We can easily determine the area of the ellipse, simply by directly applying the formula:
A = \pi \cdot a \cdot b = \pi \cdot 5 \cdot 3= 15\pi \approx 47.1238 \ u^{2}
u^{2} means square units.
Eccentricity of the ellipse
The eccentricity of the ellipse is equal to:
\epsilon = \cfrac{c}{a} = \cfrac{4}{5} = 0\text{.}8
Now let’s check the following
PF + PF' = 2a
What is P?
P is any point on the ellipse.
But how do we know exactly what is the point in the ellipse?!
Quiet, it’s very easy. All you have to do is take values for x and the value of y will be isolated, see:
Let’s take x=2 to determine that point on the ellipse and substitute it in the ellipse equation:
\cfrac{(x - 6)^{2}}{5^{2}} + \cfrac{(y - 4)^{2}}{3^{2}} = 1 \ \rightarrow \ \text{Replace } x = 2 \ \rightarrow \ \cfrac{(2 - 6)^{2}}{5^{2}} + \cfrac{(y - 4)^{2}}{3^{2}} = 1
And we started solving to isolate y!
\cfrac{(2 - 6)^{2}}{25} + \cfrac{(y - 4)^{2}}{9} = 1
We solve the parenthesis of the first fraction:
\cfrac{16}{25} + \cfrac{(y - 4)^{2}}{9} = 1
We subtract the fraction of \frac{16}{25} and do the subtraction:
\cfrac{(y - 4)^{2}}{9} = 1 - \cfrac{16}{25} \ \rightarrow \ \cfrac{(y - 4)^{2}}{9} = \cfrac{9}{25}
We multiply the 9 and do the multiplication 9\times 9:
(y - 4)^{2} = \cfrac{9 \times 9}{25} \ \rightarrow \ (y - 4)^{2} = \cfrac{81}{25}
Now we take square root on both sides of the expression to remove the square from the parentheses:
y - 4 = \cfrac{9}{5}
And finally, we add 4 to the fraction:
y = 4 + \cfrac{9}{5}
Keep in mind that this result will only give us one point of the ellipse for that value of x=2, so what you have to do is the following:
y = 4 \pm \cfrac{9}{5}
And that means that the two points that we are going to have from the ellipse for the value of x=2 are:
P_{x=2, 1}(2,5\text{.}8) \quad P_{x=2,2}(2,2\text{.}2)
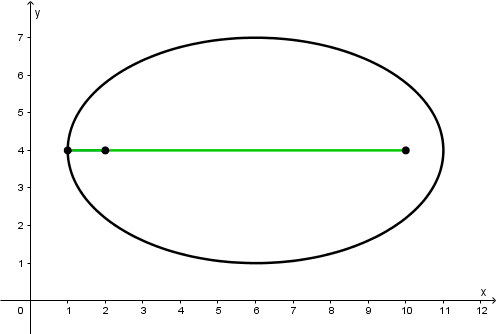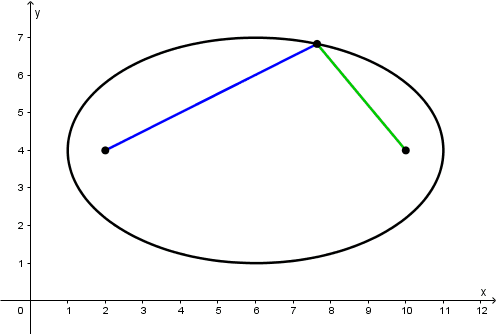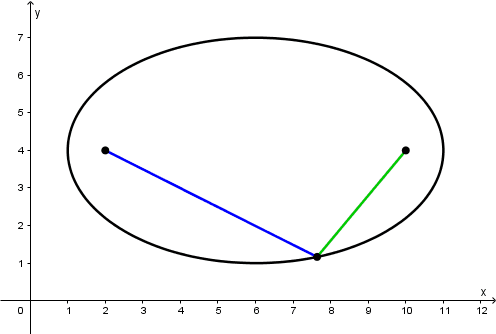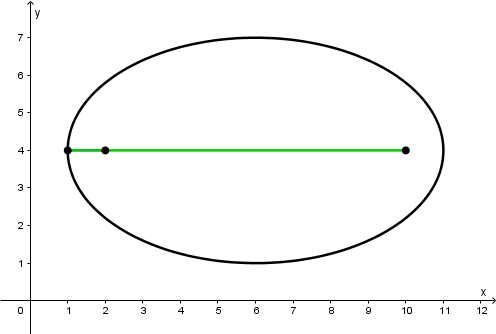
But we are only going to take one point, the P_{x=2, 1}(2,5\text{.}8), which we will simply call P. Graphically it will look as follows:
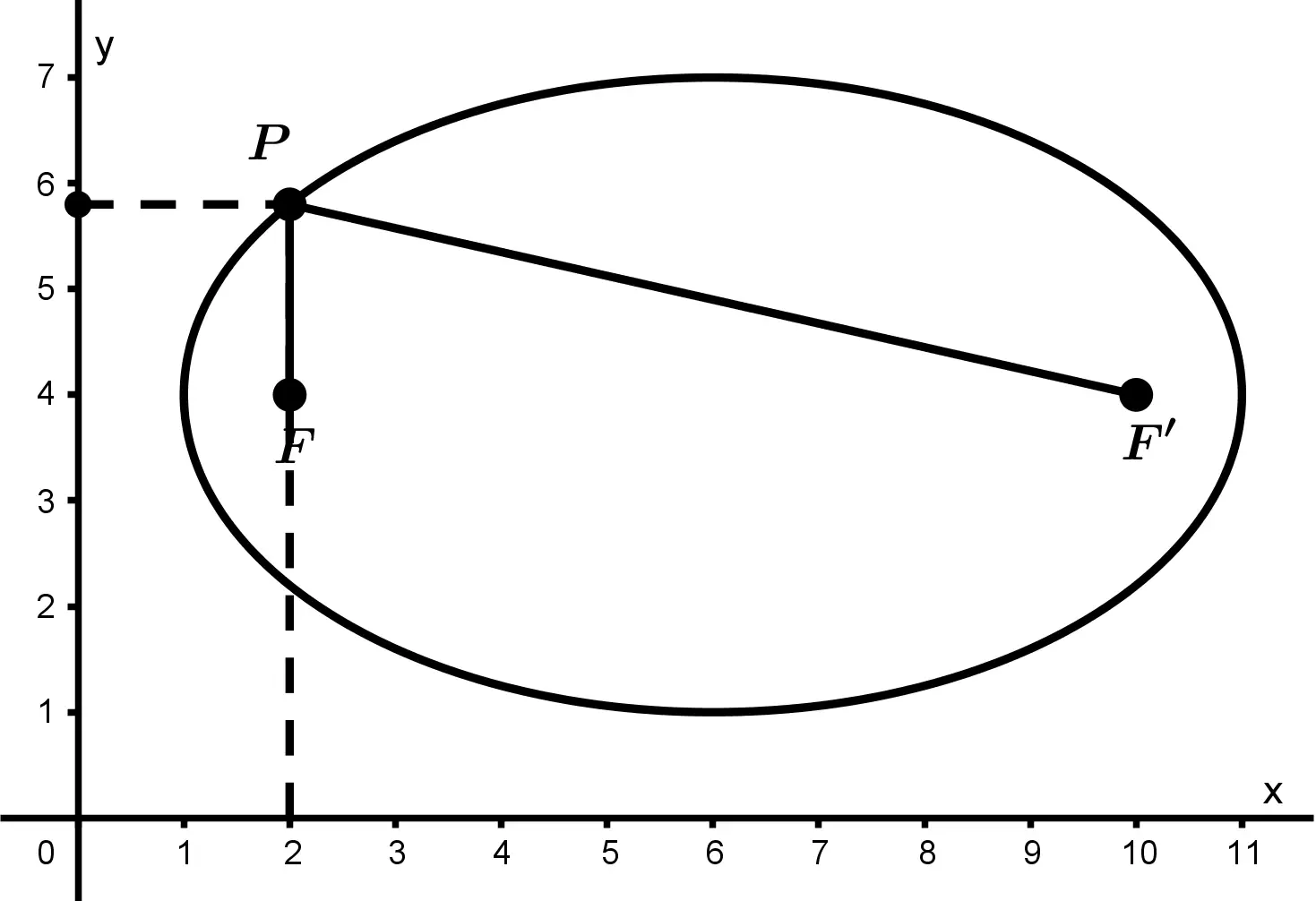
We can easily determine the lengths of \overline{PF} and \overline{PF'} because what we obtained is a right triangle!
What is the value of the \overline{PF} segment?
Its value is 1.8 because from the point F(2,4) to P(2,5.8) we only subtract 5.8 minus 4 to get that length that is equal to 1.8.
What is the value of the \overline{PF'} segment?
Because it is a right triangle and we already have the value of the \overline{PF} segment, only the value of the \overline{FF'} segment is missing which is equal to 2c because the distance from the center to each focus is equal to 4, then the value of the \overline{FF'} segment is 8.
So the value of the segment \overline{PF'} is equal to (applying the Pythagorean theorem):
\overline{PF'} = \sqrt{\left(\overline{PF}\right)^{2} + \left(\overline{FF'}\right)^{2}} = \sqrt{1\text{.}8^{2} + 8^{2}} = \cfrac{41}{5} = 8\text{.}2
\overline{PF'} is equal to 8.2
Now we go with the interesting …
What is the value of 2a?
2a is equal to 10.
So how much is the sum of segment \overline{PF} (1.8) plus \overline{PF'} (8.2)?
\overline{PF} + \overline{PF'} has a value of 10.
And done, checked!
\overline{PF}+\overline{PF'} is equal to 2a.
Thank you for being in this moment with us : )