A little further down you will find images of the elements of the circumference:
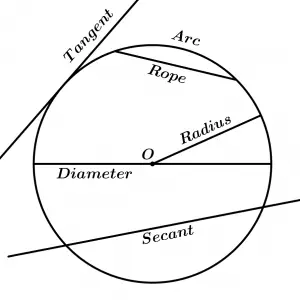
Radius of a circumference
Straight segment whose length goes from the center of the circumference to any point of it, the radius represents a constant distance from the center to any point on the circumference.
Arc of circumference
Portion of the circumference between two points of it.
Rope of a circumference
The rope is a segment of line that joins any pair of points on the circumference, in addition, the ends of the rope will be the ends of a bow. It is worth mentioning that a string subtends two arcs, one smaller than the other (unless it is the diameter where the two arcs are equal), but usually we will always refer to the smaller arc unless some other arc is specified.
Diameter of a circumference
It is the largest possible rope to draw on the circumference because it is a rope that contains the center of the circumference.
Tangent of a circumference
The tangent is a straight line that touches the circumference only at a point, so that the point where the tangent line touches the circumference is known as the point of tangency.
Secant of the circumference
The secant is a line that cuts the circumference at any two points.
\text{Circumference with center in } \ O
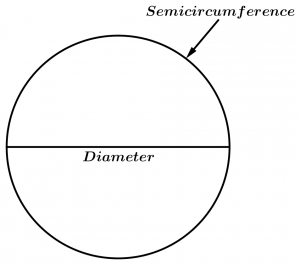
Semicircumference
The semicircumference subtends the ends of the diameter, this means that it is an arc equal to half the same circumference.
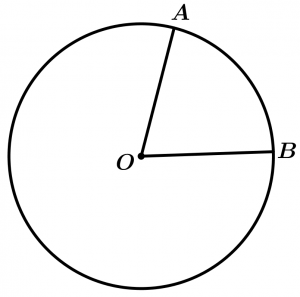
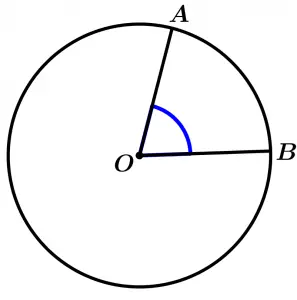
Central angle of the circumference
It is any angle whose sides are radius of the circumference.
\measuredangle AOB \ \text{ is a central angle}
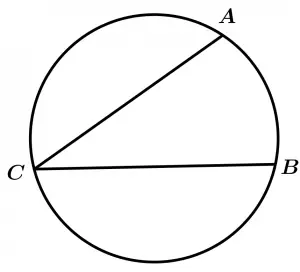
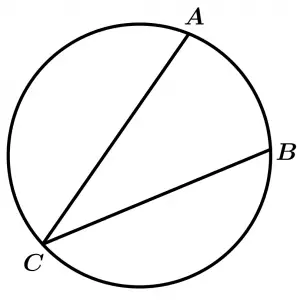
Inscribed angle of the circumference
An angle whose vertex is on the circumference and its sides are ropes of the circumference. This angle is inscribed in the arch that contains the vertex.
\measuredangle ACB \ \text{ is inscribed in the arc} \ ACB
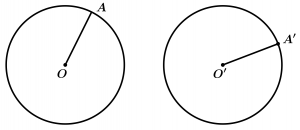
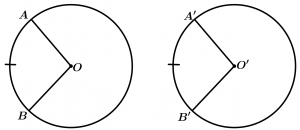
Congruent Circumferences
Two circumferences are congruent when they have a radius of the same length.
\text{If } \ \overline{OA} = \overline{ O'A'}
\text{then } \ \odot O \cong \odot O'
Theorems of the measure of the angles of the circumference
Theorem 1
The measurement of a central angle is equal to the measure of the arc intercepted by its sides.
\measuredangle AOB = \stackrel{\textstyle\frown}{AB}
Theorem 2
The measure of an inscribed angle is equal to half the measure of the arc intercepted by its sides.
\measuredangle ACB = \cfrac{\stackrel{\textstyle\frown}{AB}}{2}
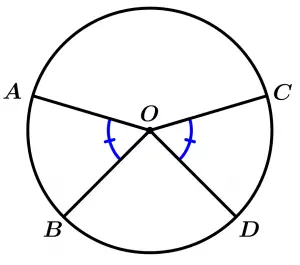
Theorem 3
The congruent central angles intercept congruent arcs in the same circumference or in congruent circumferences.
\text{If } \ \measuredangle AOB \cong \measuredangle COD \ \text{ then}
\stackrel{\textstyle\frown}{AB} \cong \stackrel{\textstyle\frown}{DC}
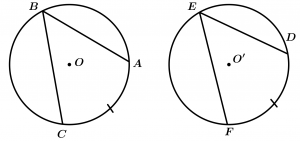
Theorem 4
Congruent arcs subtend congruent central angles in a congruent circumference or circumferences.
\text{If } \ \odot O \cong \odot O' \ \text{ y } \ \stackrel{\textstyle\frown}{AB} \cong \stackrel{\textstyle\frown}{A'B'}
\text{then } \ \measuredangle AOB \cong \measuredangle A'O'B'
Theorem 5
Congruent inscribed angles intersect congruent arcs in a circle or in congruent circles.
\text{If } \ \measuredangle ABC \cong \measuredangle DEF \ \text{ then}
\stackrel{\textstyle\frown}{AC} \cong \stackrel{\textstyle\frown}{DF}
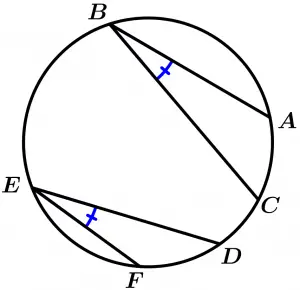
Theorem 6
The congruent arcs determine congruent inscribed angles in the same circumference or in congruent circles.
\text{If } \ \odot O \cong \odot O' \ \text{ and } \ \stackrel{\textstyle\frown}{AC} \cong \stackrel{\textstyle\frown}{DF}
\text{then } \ \measuredangle ABC \cong \measuredangle DEF
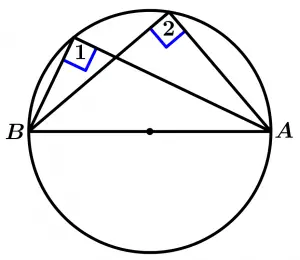
Theorem 7
Every inscribed angle that has the sides of the angle at each point of the diameter, forms right angles.
\text{If } \ \overline{AB} \ \text{ is diameter, } \ \stackrel{\textstyle\frown}{AB}
\text{is a semicircle}
\text{then } \ \measuredangle 1 = \measuredangle 2 = 90°
Theorem 8
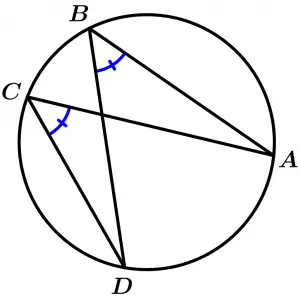
The inscribed angles that share the same arc, are congruent.
\measuredangle ABD \cong \measuredangle DCA
Theorem 9
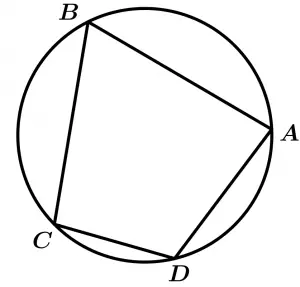
If we have a quadrilateral inscribed in a circle, its opposite angles are supplementary.
\measuredangle A + \measuredangle C = 180°
\measuredangle D + \measuredangle B = 180°
Thank you for being at this moment with us:)