For the congruence of triangles we have three criteria to indicate that really two or more triangles are congruent, these are the criteria of congruence SAS (side-angle-side), the criterion ASA (angle-side-angle) and the SSS (side-side-side) criterion.
It should be noted that some authors call them “postulates of congruence”, and others, “theorems of congruence”; but remember that it is only a question of agreements according to the level of formalism of the course: these variations do not affect the concepts in their usefulness. (Colonia, 2004, 65).
Criteria of congruence
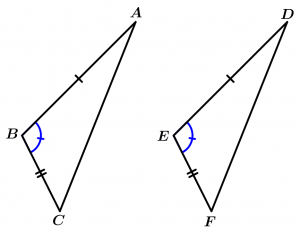
Criteria SAS (side-angle-side)
Two triangles are congruent if they respectively have two sides congruent and the angle between the two sides mentioned.
\Delta ABC \cong \Delta DEF
\overline{AB} \cong \overline{DE}
\measuredangle B \cong \measuredangle E
\overline{BC} \cong \overline{EF}
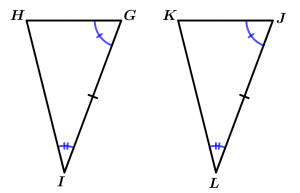
Criteria ASA (angle-side-angle)
Two triangles are congruent if they respectively have two angles congruent and the side between both angles.
\Delta GHI \cong \Delta JKL
\measuredangle G \cong \measuredangle J
\measuredangle I \cong \measuredangle L
\overline{GI} \cong \overline{JL}
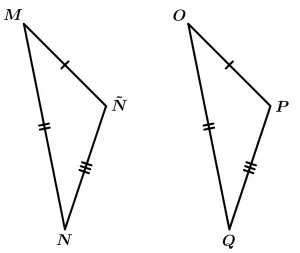
Criteria SSS (side-side-side)
Two triangles are congruent if they have three sides congruent respectively.
\Delta MNÑ \cong \Delta OPQ
\overline{M\tilde{N}} \cong \overline{OP}
\overline{MN} \cong \overline{OQ}
\overline{N\tilde{N}} \cong \overline{QP}
And that’s it, those are the criteria of congruence of triangles.
Thank you for being with us at this time:)