Welcome again, in this exercise we are going to find the equation of a parabola which we only have the vertex and the focus.
We are going to find the equation of the parabola that has the point V(3,2) of vertex and the point F(3,4) of focus.
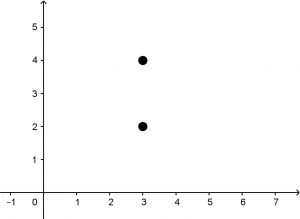
In this type of exercises it is highly recommended to graph the data that the problem offers, so in a Cartesian plane we are going to locate the vertex and the focus of the parabola.
Figure 1. V(3,2) \quad F(3,4).
Once we have the focus and the vertex located in the Cartesian plane, if we know the parabolas well, that means that our parabola opens up, look at the Figure 2:
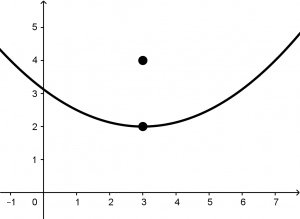
The parabola of the Figure 2 corresponds to the following equation:
(x - x_{0})^{2} = 4p(y-y_{0})
Remembering that the vertex is represented as V(x_{0}, y_{0}) and that our vertex is V(3,2), we are going to substitute these values in the equation of the parabola:
(x-3)^{2} = 4p(y-2)
How do we calculate the p from the parabola equation?
Noting that the focus is F(3,4) and that by breaking down the y coordinate of the focus, we would obtain that the focus coordinate is:
F(x_{0},y_{0} + p)
This occurs because the focus is the location of the vertex plus the distance p.
As we already have the value of y_{0} that is 2 and the value of the focus that is 4, let’s do the following to be able to find p, let’s match y_{0}+p with 4:
y_{0}+p = 4
2+p = 4
p = 2
Now all you have to do is replace that value of p in the equation of the parabola to get the equation of your parabola!
(x-3)^{2} = 8(y - 2)
The result obtained is the canonical form of the parabola equation.
Thank you for being at this moment with us : )