La definición de mediatriz
Se le llama mediatriz a la recta perpendicular trazada sobre un lado en el punto medio. Si todas las mediatrices de un polígono cortan en un mismo punto, se le conoce como circuncentro. Todos los triángulos tienen circuncentro y no todos los polígonos como los cuadriláteros, pentágonos, etc. tienen circuncentro.
Vamos con los ejemplos de las mediatrices
Para estos ejemplos de mediatrices trabajaremos con triángulos porque son sencillos, sólo tienen 3 lados y se pueden hacer cosas interesantes con ellos. Nuestros triángulos son los siguientes:
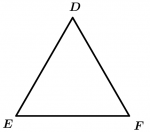
Triángulo equilátero
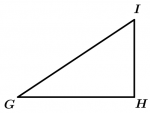
Triángulo rectángulo
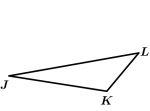
Triángulo escaleno
\overline{DE} = \overline{EF} = \overline{FD}
\measuredangle GHI = 90^{\text{o}}
\overline{JK} \neq \overline{KL} \neq \overline{LJ}
Ahora en el punto medio de cada lado de cada triángulo trazaremos un segmento perpendicular a cada lado, veamos primero las mediatrices del triángulo equilátero:
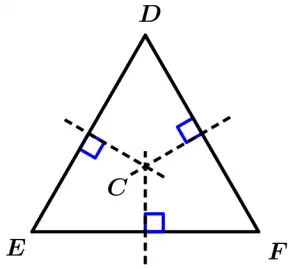
Ahora la mediatriz de cada lado del triángulo rectángulo:
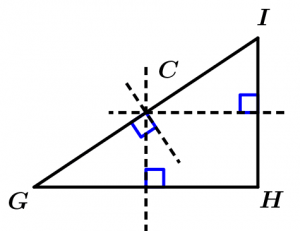
Ahora vamos con el del triángulo escaleno:
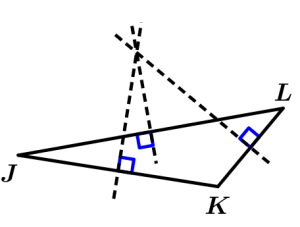
Ahora vamos a observar algo muy interesante: el punto donde se intersecan las mediatrices es conocido como circuncentro, que es el centro de una circunferencia que pasa por los vértices del triángulo, lo que quiere decir que la distancia de cada vértice del triángulo al circuncentro es igual al radio de la circunferencia, así que desde cualquier vértice del triángulo hasta el circuncentro tendremos la misma distancia, además se puede observar que tendremos un triángulo inscrito. Veamos unos ejemplos con los triángulo anteriores, tracemos la circunferencia de nuestro triángulo equilátero:
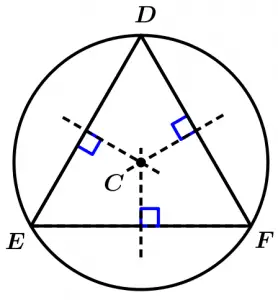
Tracemos la circunferencia del triángulo rectángulo:
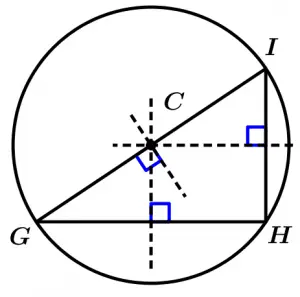
Finalmente tracemos la circunferencia del triángulo escaleno:
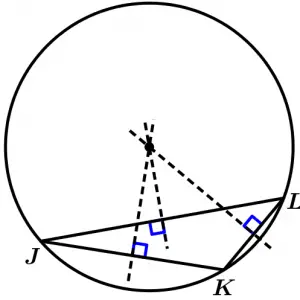
¿No te parece sorprendente? Con esto que vimos podemos mencionar algunas aplicaciones que tienen las mediatrices que sirven para determinar los circuncentros de los polígonos regulares como cubos, pentágonos, hexágonos, etc., pero igual hay muchos polígonos irregulares que sí tienen circuncentro y por lo tanto son inscritos. Si se intenta buscar las mediatrices de algún polígono irregular nos daremos cuenta que no ocurre una intersección de todas las mediatrices, así que simple y sencillamente no hay circuncentro. Por ejemplo, veamos el siguiente polígono irregular y busquemos la mediatriz de un polígono:
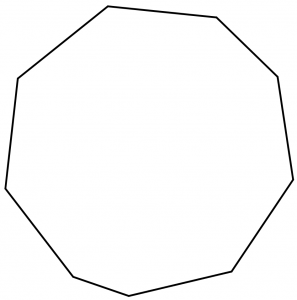
Tracemos las mediatrices del nonágono:
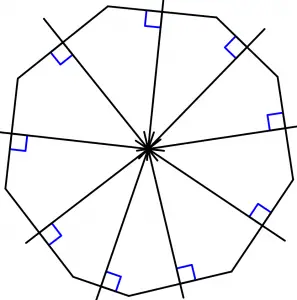
Ahora lo que veremos es una circunferencia que pasa por cada uno de los vértices del nonágono:
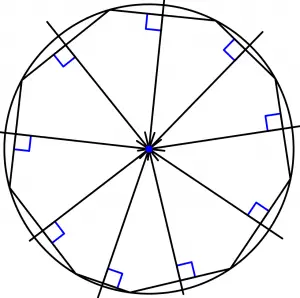
Así que ya vimos que no se necesita que un polígono sea regular para que tenga circuncentro, nuestro nonágono tiene circuncentro y es un polígono irregular, finalmente recordemos que no todos los polígono irregulares tienen circuncentro.
Gracias por estar en este momento con nosotros : )