Elipse con centro en C(x_{0},y_{0}) y con eje mayor paralelo al eje x
Veamos nuestra figura base de la elipse con la que definiremos las fórmulas de la elipse:
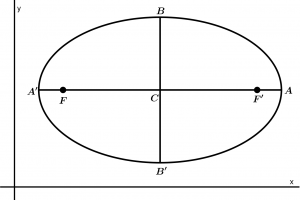
Ecuación de la elipse en coordenadas rectangulares:
La ecuación de la elipse es muy parecida a la ecuación de la hipérbola, la única diferencia es que el signo negativo que aparece entre las fracciones de la hipérbola, ahora es positivo, lo que da como resultado una elipse.
\cfrac{(x - x_{0})^{2}}{a^{2}} + \cfrac{(y - y_{0})^{2}}{b^{2}} = 1
El cual x_{0} y y_{0} representan el centro de la elipse ubicado en el plano cartesiano.
a representa la mitad de la longitud del eje mayor
b representa la mitad de la longitud del eje menor
Longitud del eje mayor de la elipse
La longitud del eje mayor de la elipse es \overline{A'A} = 2a
Donde a es la distancia que hay del centro C a A o a A'
Longitud del eje menor de la elipse
La longitud del eje menor de la elipse es \overline{B'B} = 2b
Donde b es la distancia que hay del centro C a B o a B'
Área de la elipse
El área de la elipse se calcula con la siguiente fórmula:
A = \pi \cdot a \cdot b
En el cual:
a es la mitad de la longitud del eje mayor
b es la mitad de la longitud del eje menor
Distancia del centro a los focos (c)
La longitud que hay del centro C a los focos F o F' es
c = \sqrt{a^{2} \ - b^{2}}
Excentricidad de la elipse
La fórmula para calcular la excentricidad de la elipse es la siguiente:
\epsilon = \cfrac{c}{a} = \cfrac{\sqrt{a^{2} - b^{2}}}{a}
La excentricidad sólo puede tomar valores entre 0 y 1 \ \rightarrow \ 0 < \epsilon < 1, pero ahora:
¿Qué significa la excentricidad en la elipse o qué representa?
La excentricidad representa qué tan alargada está una elipse, quiere decir que mientras una elipse tenga una excentricidad cercana al valor de 1 más alargada estará, si la excentricidad fuera igual a 1, ¡no habría elipse, sería una recta! Mientras el valor de la excentricidad tenga un valor más cercano a cero más se parecerá a una circunferencia.
Si resulta que calculas la excentricidad de una “elipse” y te da igual a cero, ¡es una circunferencia!
Ejemplo de una elipse con centro C(x_{0},y_{0}) y con eje mayor paralelo al eje x
La ecuación de la elipse es:
\cfrac{(x - 6)^{2}}{5^{2}} + \cfrac{(y - 4)^{2}}{3^{2}} = 1
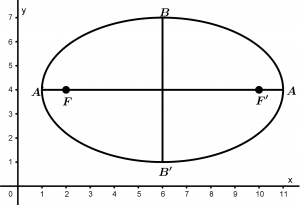
Como vemos, el denominador donde se encuentran las x es mayor que donde se encuentra la y, si pasa eso entonces tendremos una elipse horizontal. En cambio, si resulta que el denominador de las x es menor al de la y, entonces tendremos una elipse vertical. Así es como podemos diferenciar entre una elipse horizontal y vertical.
El centro de la elipse
Como se puede observar, el centro C de la elipse se encuentra en el punto:
C(6,4)
Eso quiere decir que el centro de nuestra elipse se encontrará en los valores que tenga x_{0} y y_{0} sólo que colocaremos el signos contrario en nuestra coordenada, eso quiere decir que como nuestro valor de x_{0} es -6 y nuestro valor de y_{0} es -4, entonces nuestra coordenada del centro de la elipse será C(6,4).
Longitud del eje mayor de la elipse
La longitud del eje mayor \overline{A'A} es igual a 10, lo que quiere decir que la longitud de a que es la longitud de \overline{CA} o de \overline{CA'} es igual a 5.
Longitud del eje menor de la elipse
La longitud del eje menor \overline{B'B} es igual a 6, lo que quiere decir que la longitud de b que es la longitud de \overline{CB} o de \overline{CB'} es igual a 3.
Distancia del centro a los focos de la elipse
La distancia del centro C a cualquiera de los dos focos, ya sea F o F' es:
c = \sqrt{5^{2} - 3^{2}} = \sqrt{25 - 9} = \sqrt{16} = 4
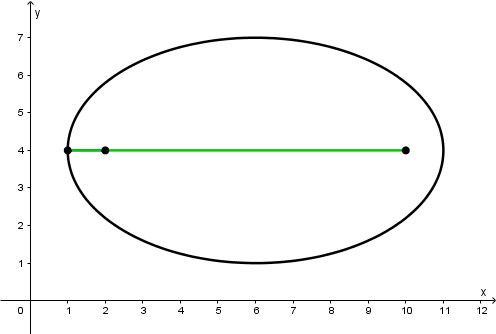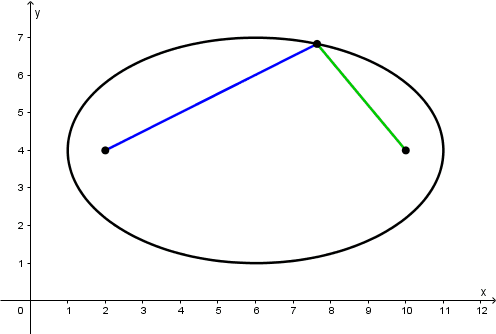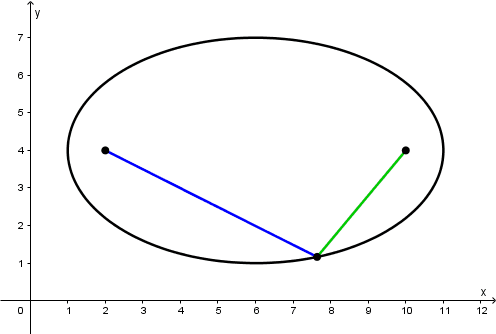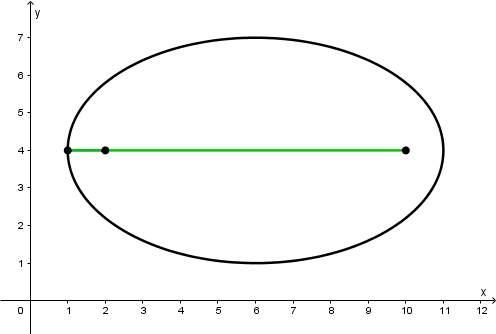
Lo que quiere decir que el foco F está en el punto F(2,4) y el foco F' está en el punto F'(10,4)
Área de la elipse
Fácilmente podemos determinar el área de la elipse, simplemente aplicando directamente la fórmula:
A = \pi \cdot a \cdot b = \pi \cdot 5 \cdot 3= 15\pi \approx 47.1238 \ u^{2}
u^{2} significa unidades cuadradas.
Excentricidad de la elipse
La excentricidad de la elipse es igual a:
\epsilon = \cfrac{c}{a} = \cfrac{4}{5} = 0\text{.}8
Ejemplo de elipse. Ahora vamos a comprobar lo siguiente
PF + PF' = 2a
¿Qué es P?
P es cualquier punto sobre la elipse.
¡¿Pero cómo sabemos exactamente cuál es un punto sobre la elipse?!
Tranquilo, es muy fácil. Lo único que se tiene que hacer es tomar valores para x y el valor de y va a salir despejando, observa:
Tomemos x = 2 para determinar ese punto sobre la elipse y sustitúyela en la ecuación de la elipse:
\cfrac{(x - 6)^{2}}{5^{2}} + \cfrac{(y - 4)^{2}}{3^{2}} = 1 \ \rightarrow \ \text{Sustituimos } x = 2 \ \rightarrow \ \cfrac{(2 - 6)^{2}}{5^{2}} + \cfrac{(y - 4)^{2}}{3^{2}} = 1
¡Y empezamos a resolver para despejar y!
\cfrac{(2 - 6)^{2}}{25} + \cfrac{(y - 4)^{2}}{9} = 1Resolvemos el paréntesis de la primera fracción:
\cfrac{16}{25} + \cfrac{(y - 4)^{2}}{9} = 1Pasamos restando la fracción de \frac{16}{25} y realizamos la resta:
\cfrac{(y - 4)^{2}}{9} = 1 - \cfrac{16}{25} \ \rightarrow \ \cfrac{(y - 4)^{2}}{9} = \cfrac{9}{25}
Pasamos multiplicando el 9 y realizamos la multiplicación 9 \times 9:
(y - 4)^{2} = \cfrac{9 \times 9}{25} \ \rightarrow \ (y - 4)^{2} = \cfrac{81}{25}
Ahora sacamos raíz cuadrada en ambos lados de la expresión para eliminar el cuadrado del paréntesis:
y - 4 = \cfrac{9}{5}
Y por último paso, pasamos sumando el 4 a la fracción:
y = 4 + \cfrac{9}{5}
Hay que tomar en cuenta que ese resultado sólo nos va a dar un punto de la elipse para ese valor de x = 2, entonces lo que se tiene que hacer es lo siguiente:
y = 4 \pm \cfrac{9}{5}
Y eso quiere decir que los dos puntos que vamos a tener de la elipse para el valor de x = 2 son:
P_{x=2, 1}(2,5\text{.}8) \quad P_{x=2,2}(2,2\text{.}2)Pero nosotros sólo vamos a tomar un punto, el P_{x=2, 1}(2,5\text{.}8), al que llamaremos simplemente P. Gráficamente se verá de la siguiente manera:
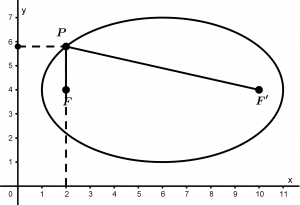
¡Fácilmente podemos determinar las longitudes de \overline{PF} y de \overline{PF'} porque lo que obtuvimos es un triángulo rectángulo!
¿Cuánto vale el segmento \overline{PF}?
Vale 1.8 porque del punto F(2,4) al P(2,5.8) sólo es restar 5.8 menos 4 para obtener esa longitud que es igual a 1.8.
¿Cuánto vale el segmento \overline{PF'}?
Como es un triángulo rectángulo y ya tenemos el valor del segmento \overline{PF}, sólo falta el valor del segmento \overline{FF'} que es igual a 2c porque la distancia del centro a cada foco es igual a 4, entonces el valor del segmento \overline{FF'} es 8.
Así que el valor del segmento \overline{PF'} es igual a (aplicando el teorema de Pitágoras):
\overline{PF'} = \sqrt{\left(\overline{PF}\right)^{2} + \left(\overline{FF'}\right)^{2}} = \sqrt{1\text{.}8^{2} + 8^{2}} = \cfrac{41}{5} = 8\text{.}2
\overline{PF'} es igual a 8.2
Ahora vamos con lo interesante…
¿Cuánto vale 2a?
2a tiene un valor de 10.
Entonces, ¿cuánto vale la suma del segmento \overline{PF} (1.8) más \overline{PF'} (8.2)?
\overline{PF}+\overline{PF'} tiene un valor de 10.
¡Y listo, comprobado!
\overline{PF}+\overline{PF'} es igual a 2a.
Gracias por estar en este momento con nosotros : )