La circunferencia es un lugar geométrico en el cual todos los puntos equidistan de un punto fijo llamado centro.
De forma matemática la circunferencia se representa por una ecuación de segundo grado:
x^{2} + y^{2} = r^{2}
Donde la ecuación anterior representa a una circunferencia que tiene como centro el origen del sistema de ejes coordenados.
Y para representar a una circunferencia con el centro fuera del origen, utilizamos la ecuación siguiente:
\left(x - (h) \right)^{2} + \left(y - (k) \right)^{2} = r^{2}
Donde h y k representan al centro de la circunferencia en \left( h, k \right).
Analicemos dos ejemplos de la circunferencia:
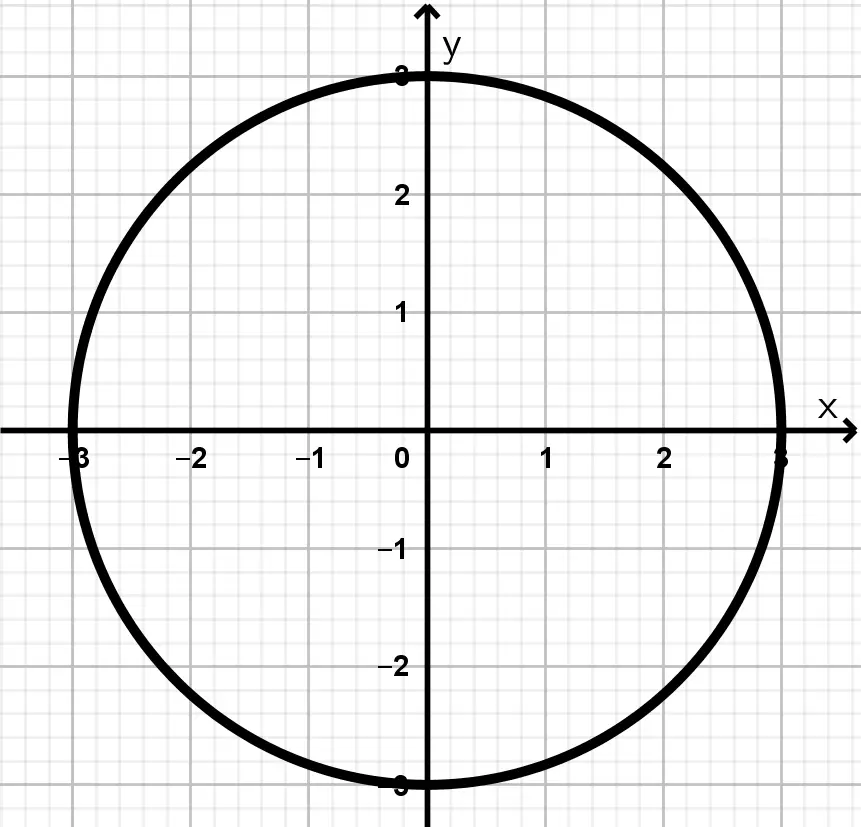
Ejemplo de circunferencia 1. Dibujar el lugar geométrico que representa la ecuación x^{2} + y^{2} = 9.
Como podemos observar en la ecuación del ejercicio, es una circunferencia que tiene como centro el origen y el radio lo tenemos que calcular, en este caso:
r^{2} = 9
Sólo tenemos que aplicar raíz cuadrada a la igualdad anterior para obtener nuestro radio:
r = 3
Finalmente podemos ubicar nuestra circunferencia en el plano cartesiano:
Figura 2. Circunferencia x^{2} + y^{2} = 9
Veamos un ejemplo donde el centro no se encuentra en el origen.
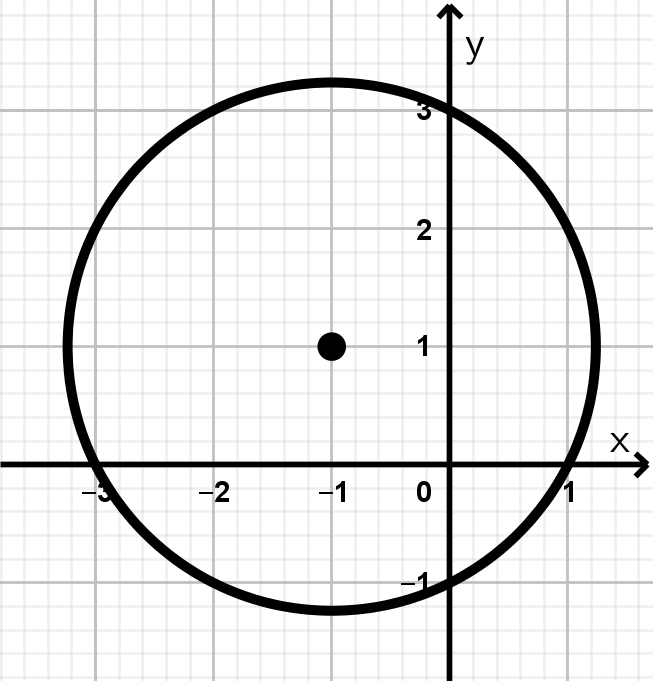
Ejemplo de una circunferencia 2. Dibujar el lugar geométrico que representa la ecuación (x + 1)^{2} + (y - 1)^{2} = 5.
Lo que podemos observar en este ejercicio es que no es una circunferencia que se encuentre en el origen, si no tenemos mucha práctica, tenemos que colocar los debidos paréntesis a la ecuación de la circunferencia como se muestra a continuación:
(x + 1)^{2} + (y - 1)^{2} = (x - (-1))^{2} + (y - (1))^{2} = 5
Perfecto, ahora que ya agregamos los debidos paréntesis, podemos decir que el centro se encuentra en el punto:
(-1 , 1)
Sólo faltaría calcular el radio de la circunferencia, para eso simplemente tenemos que aplicarle la debida raíz cuadrada al 5:
r^{2} = 5 \rightarrow r = \sqrt{5}
Y con el centro de la circunferencia y el radio ya calculados, bien podemos proceder a trazar nuestra circunferencia:
Figura 3. Circunferencia (x + 1)^{2} + (y - 1)^{2} = 5
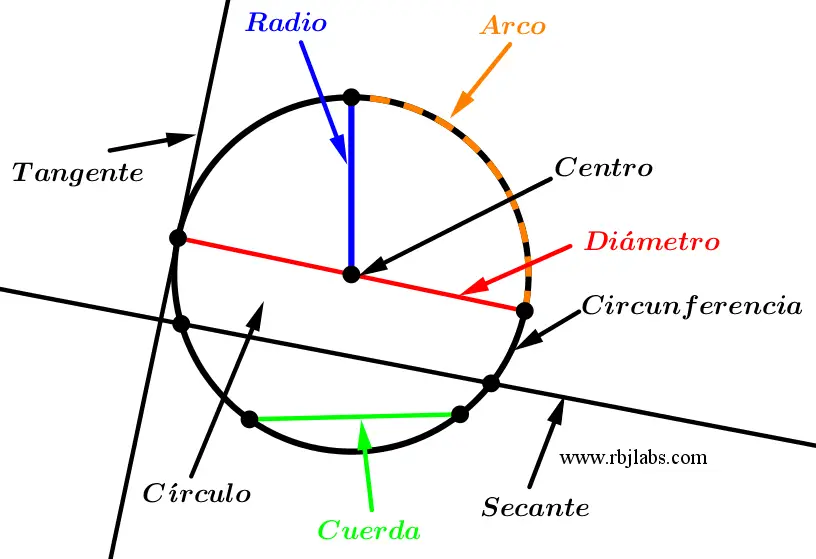
Elementos y rectas de la circunferencia
En este apartado mencionaremos las partes que conforman a una circunferencia y además mencionaremos el nombre que se le dan a las rectas o segmentos que cortan la circunferencia.
De todas formas aquí te dejo un artículo donde se explican más a detalle los elementos de la circunferencia con varios teoremas interesantes.
Radio de la circunferencia
El radio es un segmento que une el centro con cualquier punto de la circunferencia.
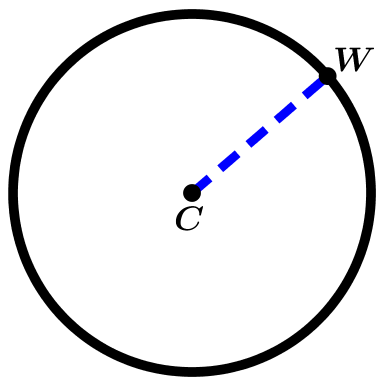
Podemos apreciar que el radio de la circunferencia es el segmento:
\overline{CW}
Diámetro de la circunferencia
El diámetro es el segmento que une dos puntos de la circunferencia pasando por el centro.
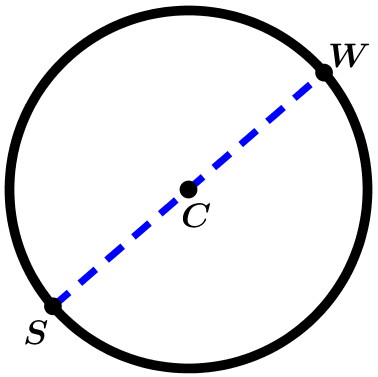
Diámetro \overline{WS} pasando a través del centro C.
Arco de la circunferencia
El arco de la circunferencia es una parte de la misma circunferencia delimitada por dos puntos cualquiera.
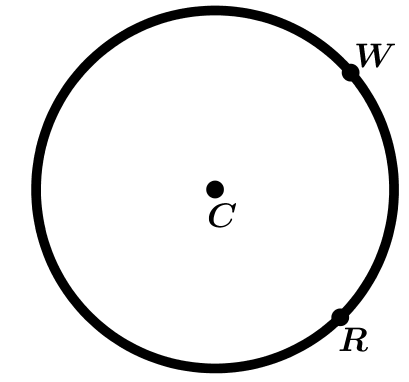
El arco se denomina como:
\text{Arco } \ \widehat{WR}
Cuerda de la circunferencia
La cuerda es un segmento que une dos puntos de la circunferencia.
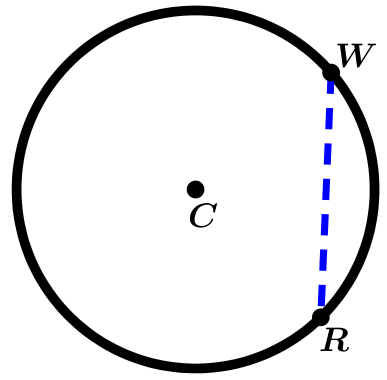
Como se aprecia en la figura anterior, la circunferencia tiene una:
\text{Cuerda } \ \overline{WR}
Recta tangente a la circunferencia
Se denomina recta tangente a la circunferencia cuando dicha recta toca a la circunferencia en un punto, recibiendo como nombre de punto de tangencia.
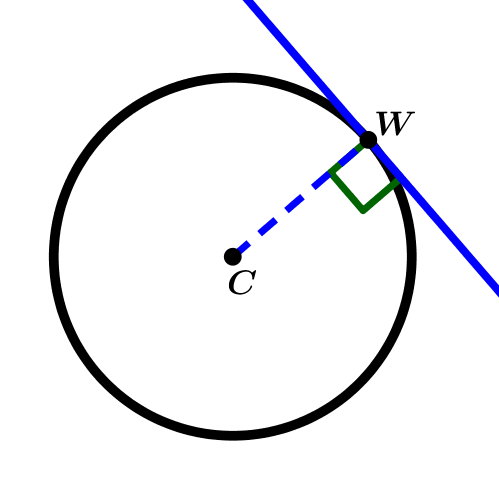
W es el punto de tangencia.
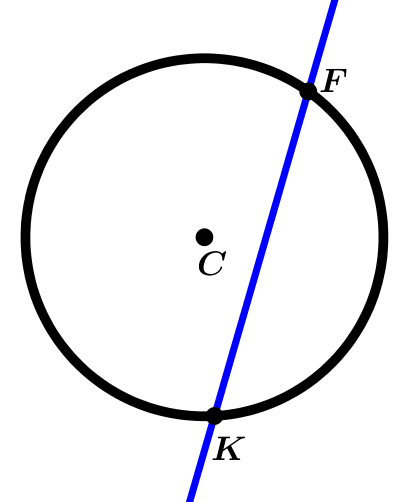
Recta secante a la circunferencia
La recta secante es dicha recta que atraviesa a la circunferencia en dos puntos, resultando en que una parte de la misma recta es cuerda de la circunferencia.
Gracias por estar en este momento con nosotros : )