Un poco más abajo encontrarás imágenes de los elementos de la circunferencia siguientes:
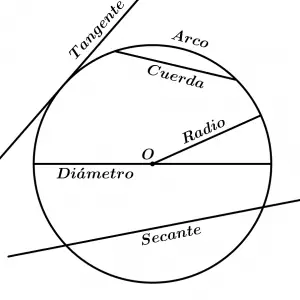
Radio de una circunferencia
Segmento recto cuya longitud va desde el centro de la circunferencia hacia un punto cualquiera de ella, el radio representa una distancia constante del centro a cualquier punto de la circunferencia.
Arco de circunferencia
Porción de la circunferencia entre dos puntos de ella.
Cuerda de una circunferencia
La cuerda es un segmento de recta que une cualquier par de puntos de la circunferencia, además, los extremos de la cuerda serán los extremos de un arco. Cabe mencionar que una cuerda subtiende dos arcos, uno más pequeño que otro (al menos que fuera el diámetro donde los dos arcos son iguales), pero por lo general siempre nos referiremos al arco más pequeño al menos que se especifique algún otro arco.
Diámetro de una circunferencia
Es la mayor cuerda posible de trazar en la circunferencia ya que es una cuerda que contiene al centro de la circunferencia.
Tangente de una circunferencia
La tangente es una línea recta que toca a la circunferencia solamente en un punto con lo cual al punto donde la recta tangente toca a la circunferencia se le conoce como punto de tangencia.
Secante de la circunferencia
La secante es una recta que corta a la circunferencia en dos puntos cualesquiera.
\text{Circunferencia con centro en } \ O
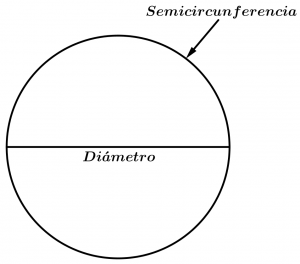
Semicircunferencia
La semicircunferencia subtiende a los extremos del diámetro, esto quiere decir que es un arco igual a la mitad de la misma circunferencia.
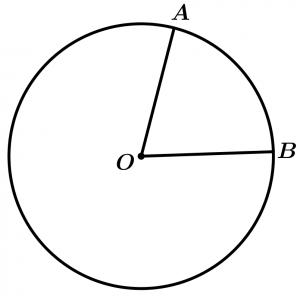
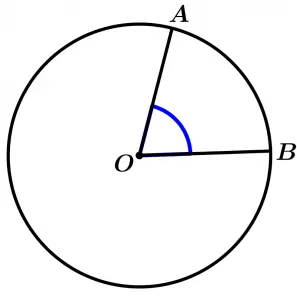
Ángulo central de la circunferencia
Es todo ángulo cuyos lados sean radios de la circunferencia.
\measuredangle AOB \ \text{ es un ángulo central}
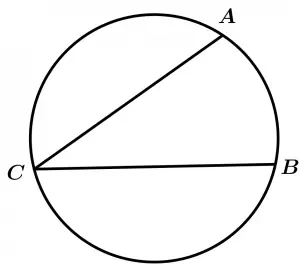
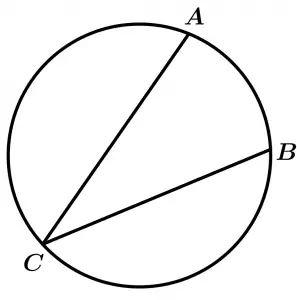
Ángulo inscrito de la circunferencia
Ángulo cuyo vértice está sobre la circunferencia y sus lados son cuerdas de la circunferencia. Este ángulo está inscrito en el arco que contiene al vértice.
\measuredangle ACB \ \text{ está inscrito en el arco} \ ACB
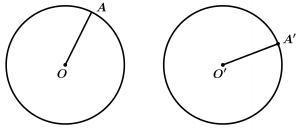
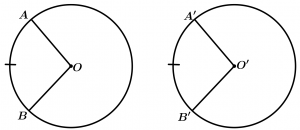
Circunferencias congruentes
Dos circunferencias son congruentes cuando tienen radios de longitud igual.
\text{Si } \ \overline{OA} = \overline{ O'A'}
\text{entonces } \ \odot O \cong \odot O'
Teoremas de la medida de los ángulos de la circunferencia
Teorema 1
La medida de un ángulo central es igual a la medida del arco que interceptan sus lados.
\measuredangle AOB = \stackrel{\textstyle\frown}{AB}
Teorema 2
La medida de un ángulo inscrito es igual a la mitad de la medida del arco que interceptan sus lados.
\measuredangle ACB = \cfrac{\stackrel{\textstyle\frown}{AB}}{2}
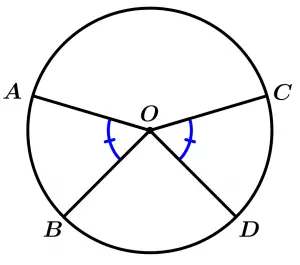
Teorema 3
Los ángulos centrales congruentes interceptan arcos congruentes en una misma circunferencia o en circunferencias congruentes.
\text{Si } \ \measuredangle AOB \cong \measuredangle COD \ \text{ entonces}
\stackrel{\textstyle\frown}{AB} \cong \stackrel{\textstyle\frown}{DC}
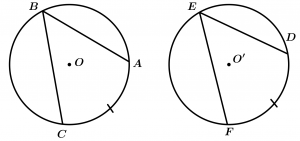
Teorema 4
Los arcos congruentes subtienden ángulos centrales congruentes en una circunferencia o en circunferencias congruentes.
\text{Si } \ \odot O \cong \odot O' \ \text{ y } \ \stackrel{\textstyle\frown}{AB} \cong \stackrel{\textstyle\frown}{A'B'}
\text{entonces } \ \measuredangle AOB \cong \measuredangle A'O'B'
Teorema 5
Los ángulos inscritos congruentes interceptan arcos congruentes en una circunferencia o en circunferencias congruentes.
\text{Si } \ \measuredangle ABC \cong \measuredangle DEF \ \text{ entonces}
\stackrel{\textstyle\frown}{AC} \cong \stackrel{\textstyle\frown}{DF}
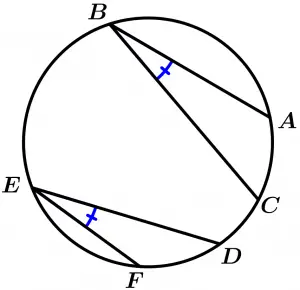
Teorema 6
Los arcos congruentes determinan ángulos inscritos congruentes en una misma circunferencia o en circunferencias congruentes.
\text{Si } \ \odot O \cong \odot O' \ \text{ y } \ \stackrel{\textstyle\frown}{AC} \cong \stackrel{\textstyle\frown}{DF}
\text{entonces } \ \measuredangle ABC \cong \measuredangle DEF
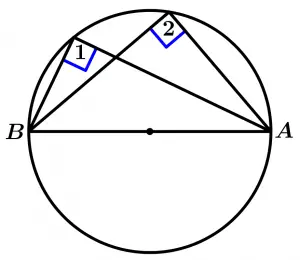
Teorema 7
Todo ángulo inscrito que tenga los lados del ángulo en cada punto del diámetro, forma ángulos rectos.
\text{Si } \ \overline{AB} \ \text{ es diámetro, } \ \stackrel{\textstyle\frown}{AB}
\text{es una semicircunferencia}
\text{entonces } \ \measuredangle 1 = \measuredangle 2 = 90°
Teorema 8
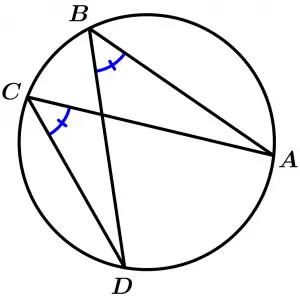
Los ángulos inscritos que compartan el mismo arco, son congruentes.
\measuredangle ABD \cong \measuredangle DCA
Teorema 9
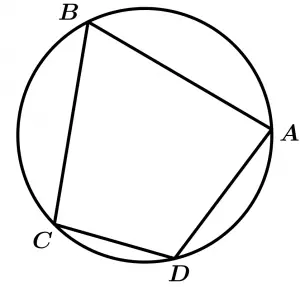
Si tenemos un cuadrilátero inscrito en una circunferencia, sus ángulos opuestos son suplementarios.
\measuredangle A + \measuredangle C = 180°
\measuredangle D + \measuredangle B = 180°
Gracias por estar en este momento con nosotros : )