Para la congruencia de triángulos tenemos tres criterios para señalar que de verdad dos o más triángulos cualesquiera son congruentes, estos son el criterio de congruencia LAL (lado-ángulo-lado), el criterio ALA (ángulo-lado-ángulo) y el criterio LLL (lado-lado-lado).
Cabe señalar que algunos autores les llaman “postulados de congruencia”, y otros, “teoremas de congruencia”; pero recuerda que sólo es cuestión de convenios acordes con el nivel de formalismo del curso: estas variaciones no afectan los conceptos in su utilidad. (Colonia, 2004, 65).
Criterios de congruencia
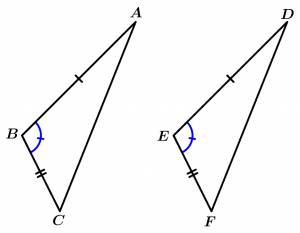
Criterio LAL (lado-ángulo-lado)
Dos triángulos son congruentes si respectivamente tienen congruentes dos lados y el ángulo comprendido entre dichos dos lados.
\Delta ABC \cong \Delta DEF
\overline{AB} \cong \overline{DE}
\measuredangle B \cong \measuredangle E
\overline{BC} \cong \overline{EF}
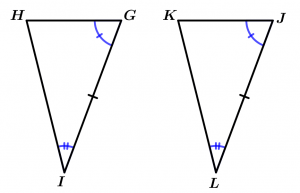
Criterio ALA (ángulo-lado-ángulo)
Dos triángulos son congruentes si respectivamente tienen congruentes dos ángulos y el lado comprendido entre dichos ángulos.
\Delta GHI \cong \Delta JKL
\measuredangle G \cong \measuredangle J
\measuredangle I \cong \measuredangle L
\overline{GI} \cong \overline{JL}
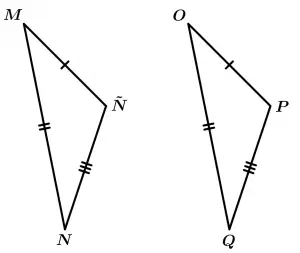
Criterio LLL (lado-lado-lado)
Dos triángulos son congruentes si respectivamente tienen congruentes los tres lados.
\Delta MNÑ \cong \Delta OPQ
\overline{M\tilde{N}} \cong \overline{OP}
\overline{MN} \cong \overline{OQ}
\overline{N\tilde{N}} \cong \overline{QP}
Y listo, esos son los criterios de congruencia de triángulos.
Gracias por estar con nosotros en este momento : )