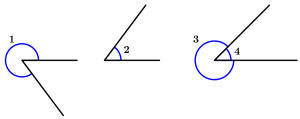Un ángulo es la abertura formada por dos rectas, semirrectas o segmentos que comparten un punto en común llamado vértice y de acuerdo con su medida y con su agrupación, podemos clasificarlos de dos maneras diferentes.
A continuación veremos los tipos de ángulos de acuerdo con su medida y de acuerdo con su agrupación.
Clasificación de los ángulos según su medida
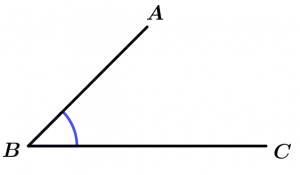
Ángulo agudo
El ángulo agudo es aquel que mide más de 0° y menos de 90°.
0° < \ \measuredangle ABC < 90°
\measuredangle ABC \ \text{ es agudo}
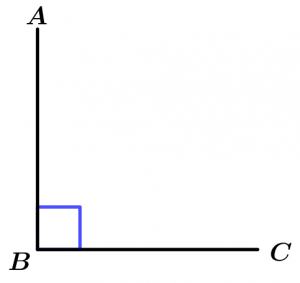
Ángulo recto
El ángulo recto es aquel que mide 90° y se suele simbolizar con un pequeño cuadrado en el vértice del ángulo.
\measuredangle ABC = 90°
\measuredangle ABC \ \text{ es ángulo recto}
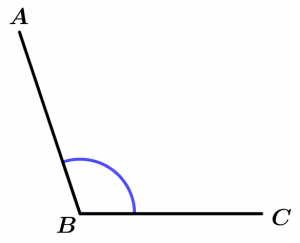
Ángulo obtuso
El ángulo obtuso es el que mide más de 90° y menos de 180°.
90° < \measuredangle ABC < 180°
\measuredangle ABC \ \text{ es obtuso}
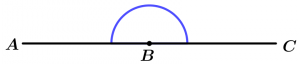
Ángulo llano o de lados colineales
El ángulo llano o de lados colineales es aquel que mide exactamente 180°.
\measuredangle ABC = 180°
\measuredangle ABC \ \text{ es llano}
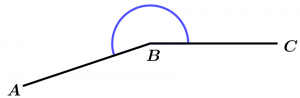
Ángulo entrante
El ángulo entrante es aquel que mide más de 180° y menos de 360°.
180° < \measuredangle ABC < 360°
\measuredangle ABC \ \text{ es entrante}
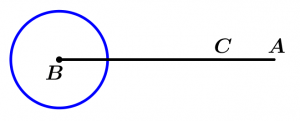
Ángulo perigonal
El ángulo perigonal es aquel que mide exactamente 360°.
\measuredangle ABC= 360°
\measuredangle ABC \ \text{ es perigonal}
Clasificación de los ángulos según su agrupación
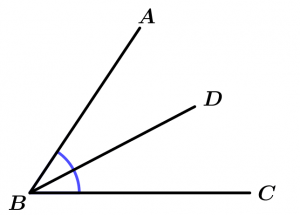
Ángulos adyacentes
Los ángulos adyacentes son dos ángulos que tienen en común un lado y un vértice.
\measuredangle ABD \ \text{ es adyacente al } \ \measuredangle DBC
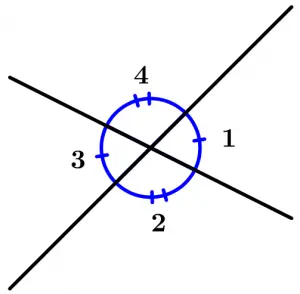
Ángulos opuestos por el vértice
Los ángulos opuestos por el vértice son aquellos los cuales los lados de un ángulo son la prolongación de los lados de otro ángulo y además son congruentes.
\measuredangle 1 \ \text{ es opuesto al } \ \measuredangle 3 \ \text{ y } \ \measuredangle 1 \cong \measuredangle 3
\measuredangle 4 \ \text{ es opuesto al } \ \measuredangle 2 \ \text{ y } \ \measuredangle 4 \cong \measuredangle 2
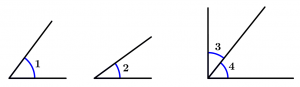
Ángulos complementarios
Los ángulos complementarios son dos ángulos cuyas medidas sumadas dan como resultado 90° y pueden ser adyacentes o no.
\measuredangle 1 + \measuredangle 2 = 90°
\measuredangle 3 + \measuredangle 4 = 90°
\measuredangle 1 \ \text{ y } \ \measuredangle 2 \ \text{ no son adyacentes y }
\measuredangle 3 \ \text{ y } \ \measuredangle 4 \ \text{ son adyacentes}
Ángulos suplementarios
Los ángulos suplementarios son dos ángulos cuyas medidas sumadas dan como resultado 180° y pueden ser adyacentes o no.
\measuredangle 1 + \measuredangle 2 = 180°
\measuredangle 3 + \measuredangle 4 = 180°
\measuredangle 1 \ \text{ y } \ \measuredangle 2 \ \text{ no son adyacentes y }
\measuredangle 3 \ \text{ y } \ \measuredangle 4 \ \text{ son adyacentes}
Ángulos conjugados
Los ángulos conjugados son dos ángulos cuyas medidas sumadas dan como resultado 360° y pueden ser adyacentes o no.
\measuredangle 1 + \measuredangle 2 = 360°
\measuredangle 3 + \measuredangle 4 = 360°
\measuredangle 1 \ \text{ y } \ \measuredangle 2 \ \text{ no son adyacentes y }
\measuredangle 3 \ \text{ y } \ \measuredangle 4 \ \text{ son adyacentes}
Gracias por estar en este momento con nosotros : )