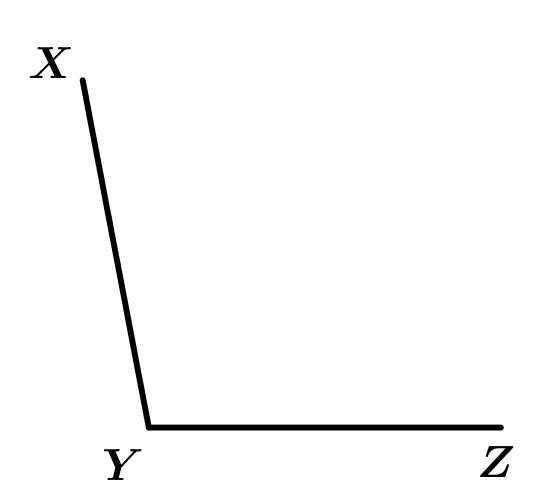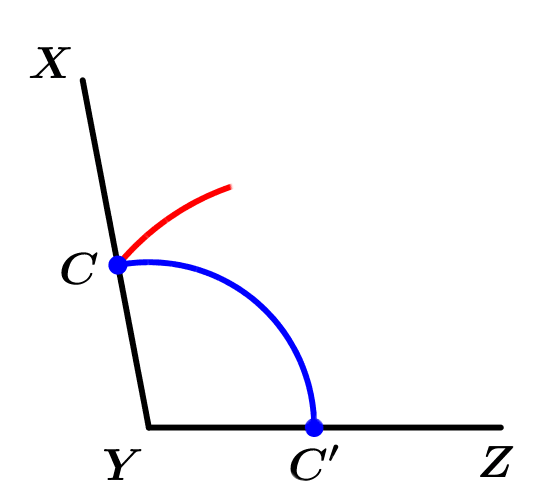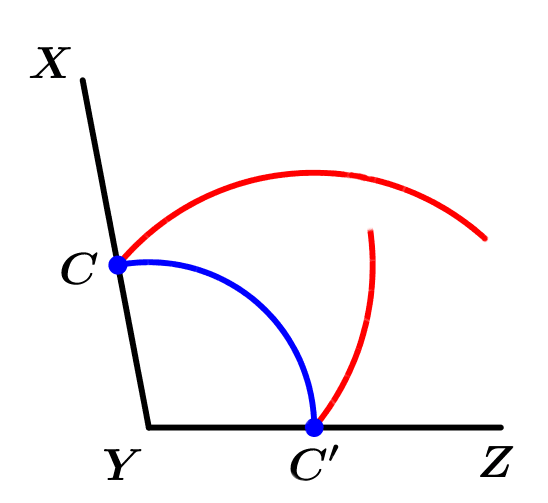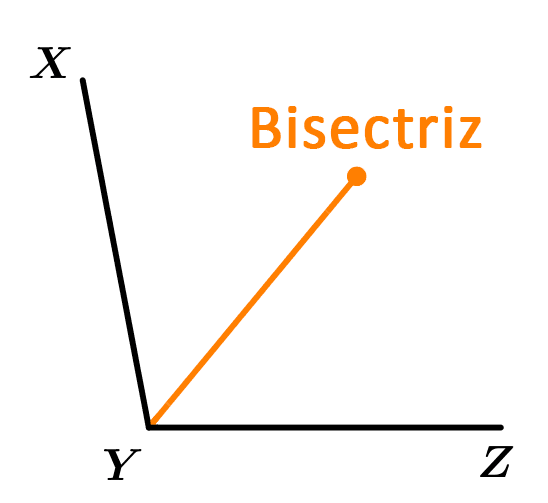La definición de bisectriz
Se le llama bisectriz de un ángulo a la recta, semirrecta o segmento que divide dicho ángulo en dos ángulos iguales. Las bisectrices de los ángulos de un polígono que se cortan en un mismo punto se llama incentro. Todos los triángulos tienen incentro y no todos los polígonos como cuadriláteros, pentágonos, hexágonos, etc. tienen incentro.
Cómo trazar una bisectriz
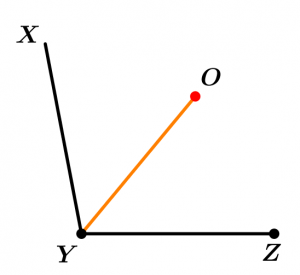
Antes de continuar con los ejemplos, quiero enseñar cómo trazar una bisectriz, sólo necesitas un compás de un buen juego de geometría. Trazaremos la bisectriz del \measuredangle XYZ.
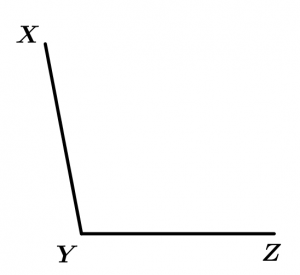 Seguidamente trazaremos un arco de circunferencia donde el punto Y será el centro y el radio puede ser del largo que gustes, así obtendremos dos intersecciones a las que llamaremos C y C':
Seguidamente trazaremos un arco de circunferencia donde el punto Y será el centro y el radio puede ser del largo que gustes, así obtendremos dos intersecciones a las que llamaremos C y C':
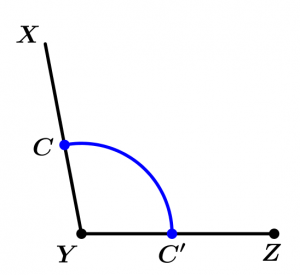 Luego trazaremos dos arcos de circunferencia más, las cuales tendrán como centros a C y a C' y de radio serán el segmento \overline{C C'} y su intersección la llamaremos O:
Luego trazaremos dos arcos de circunferencia más, las cuales tendrán como centros a C y a C' y de radio serán el segmento \overline{C C'} y su intersección la llamaremos O:
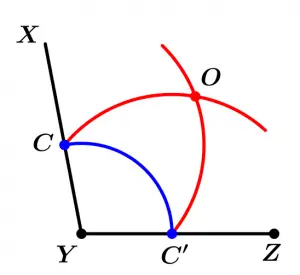 Finalmente el segmento, semirrecta o recta que se traza con los puntos Y y O es la bisectriz.
Finalmente el segmento, semirrecta o recta que se traza con los puntos Y y O es la bisectriz.
Bisectriz del \measuredangle XYZ
Gráficamente es así:
Vamos con los ejemplos de bisectriz
Aquí es todavía más necesario que tengas un buen juego de geometría. Calcularemos el incentro de un triángulo, para hacer esto hay que calcular la bisectriz de cada ángulo del triángulo. Trabajaremos con un triángulo rectángulo y con un triángulo escaleno.
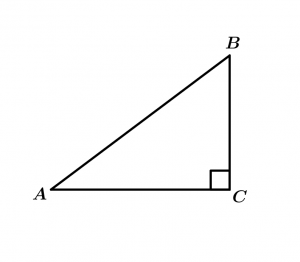
Triángulo rectángulo
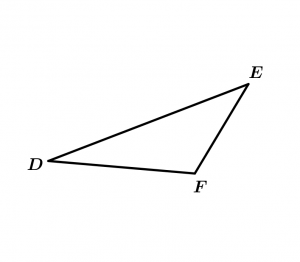
Triángulo escaleno
\measuredangle ACB = 90^{\text{o}}
\overline{DE} \neq \overline{EF} \neq \overline{FD}
Ahora tracemos las bisectrices de cada uno de los triángulos:
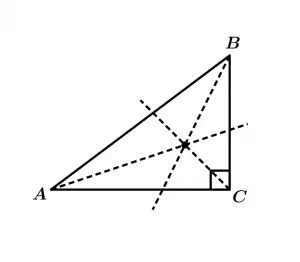
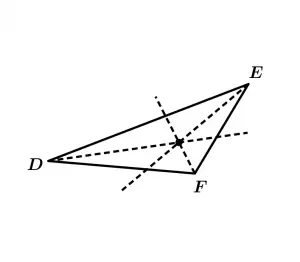
Bisectrices triángulo rectángulo
Bisectrices triángulo escaleno
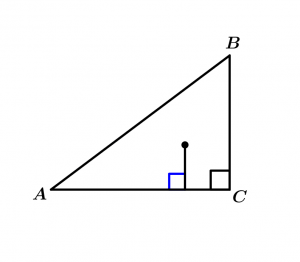
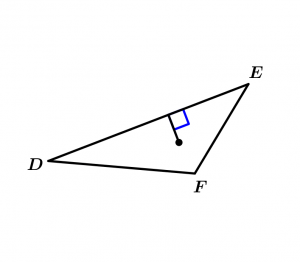
Luego tracemos un segmento que sea perpendicular en cualquiera de los lados del triángulo, este segmento será el radio de nuestra circunferencia:
Radio de la circunferencia inscrita en el triángulo rectángulo
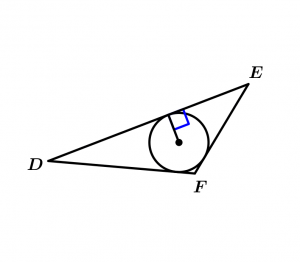
Radio de la circunferencia inscrita en el triángulo escaleno
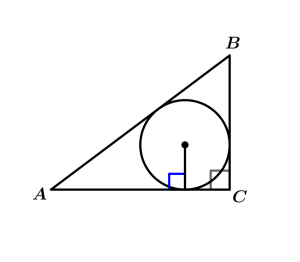
Ahora simplemente trazamos nuestra circunferencia inscrita:
Circunferencia inscrita en triángulo rectángulo
Circunferencia inscrita en triángulo escaleno
Eso es todo, ya sabes cómo trazar el incentro de cualquier triángulo.
Recuerda: si un polígono tiene incentro, tiene circunferencia inscrita; si un polígono tiene circunferencia inscrita, tiene incentro.
Unos ejemplos más
Primero quiero recalcar que TODOS los polígonos regulares tienen incentro.
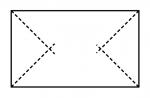
A continuación veremos unos cuadriláteros. Te darás cuenta que hay cuadriláteros irregulares que tienen incentro y otros que no. Las líneas punteadas del cuadrilátero sin incentro son las bisectrices.
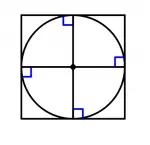
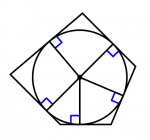
Cuadrilátero regular con incentro
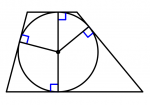
Cuadrilátero irregular con incentro
Cuadrilátero sin incentro
A continuación veremos unos pentágonos. Te darás cuenta que hay pentágonos irregulares que tienen incentro y otros que no. Las líneas punteadas del pentágono sin incentro son las bisectrices.
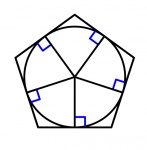
Pentágono regular con incentro
Pentágono irregular con incentro
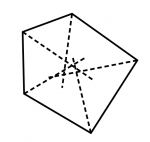
Pentágono irregular sin incentro
Y como te habrás dado cuenta, todos los polígonos regulares tienen incentro y hay polígonos irregulares que tienen y no tienen incentro.
¡Ya estás listo para salir al mundo y calcular bisectrices e incentros!
Gracias por estar en este momento con nosotros : )