Área del triángulo
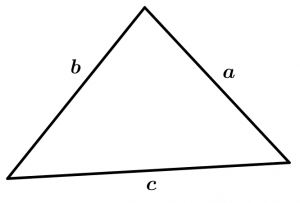
Para el cálculo del área del triángulo, utilizaremos la famosa fórmula de base por altura sobre dos:
A = \cfrac{b\cdot h}{2}
Y vamos a ver 3 formas en las que se nos pueden presentar los triángulos al momento de aplicar la fórmula mencionada ya que a veces el cerebro nos engaña.
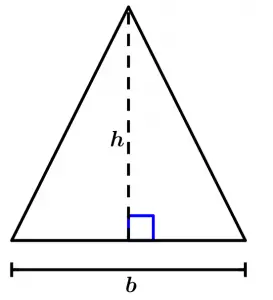
Primera forma
Esta primera forma es cuando el triángulo se le puede trazar una altura que esté encima de la base y no en las esquinas de la base o fuera de la base.
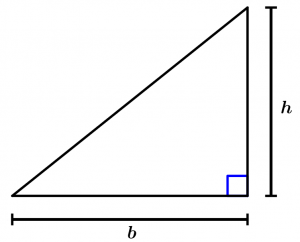
Segunda forma
La segunda forma es cuando se te presenta un triángulo rectángulo, el cual su altura es su mismo cateto vertical.
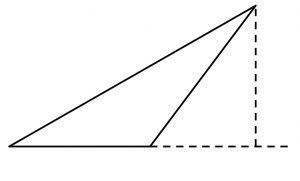
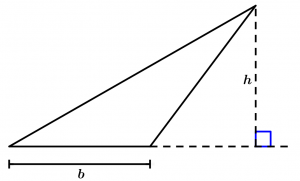
Tercera forma
La tercera forma es cuando se presenta un triángulo al cual no sabemos cómo trazarle una altura, para hacer eso extenderemos imaginariamente la longitud de la base (pero la base va a valer lo mismo) hasta que forme una línea perpendicular con el punto más alto, y una vez que ya tengamos la altura sólo aplicamos la fórmula antes mencionada.
Fórmula de Herón
No podemos dejar pasar la fórmula de Herón, donde tenemos un semiperímetro que nos ayudará a escribir la fórmula, el semiperímetro Sp simplemente es el perímetro del triángulo dividido entre 2:
Sp = \cfrac{a + b + c}{2}
Y la fórmula de Herón para calcular el área de un triángulo es la siguiente:
A = \sqrt{Sp\left(Sp - a \right) \left(Sp - b \right) \left(Sp - c\right)}
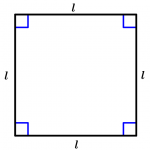
Área del cuadrado
El área del cuadrado es igual al cuadrado de cualquiera de sus lados (l):
A = l^{2}
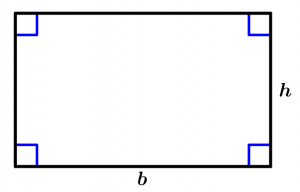
Área del rectángulo
El área de un rectángulo es igual al producto de la base (b) por la altura (h):
A = b\cdot h
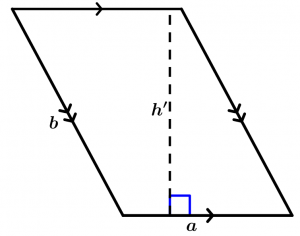
Área del paralelogramo
Un paralelogramo con lados a, b y altura h tienen un área igual al producto de uno de sus lados por la altura correspondiente a ese lado.
En el siguiente paralelogramo observamos que el área es el lado b (que hace función de base) multiplicado por la altura (h) de ese lado:
A = b\cdot h
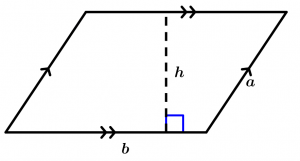La siguiente figura que observaremos es el mismo paralelogramo sólo que rotado, veremos como es que la altura cambia debido a que ahora la base es el lado a:
A = a\cdot h'
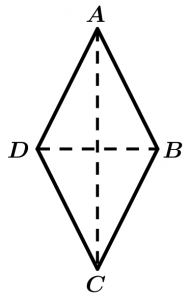
Área del rombo
El área del rombo es igual a la mitad del producto de sus diagonales:
A = \cfrac{\left( AC\right) \left(DB \right)}{2}
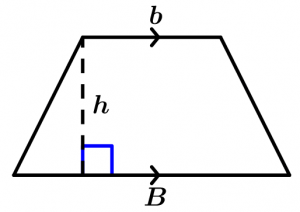
Área del trapecio
El área del trapecio es igual a la semisuma de sus lados paralelos multiplicada por su altura:
A = \left(\cfrac{B + b }{2}\right)h
Área de polígonos regulares
El área de un polígono regular es su perímetro (P) multiplicado por el apotema (a) dividido entre dos:
A = \cfrac{P\cdot a}{2}
Cuando hablamos de polígonos regulares igual hablamos de hexágonos, heptágonos, octágonos, n-ágonos regulares.
Ejemplo del cálculo del área de un nonágono regular
El siguiente nonágono regular tiene un apotema a de 2.06 cm y su lado l mide 1.5 cm, calcula su área:
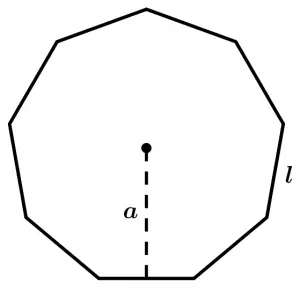El perímetro del nonágono se calcula multiplicando la longitud del lado l por su cantidad de lados, que en este caso es 9:
P = l\cdot 9 = 1.5 \cdot 9 = 13.5 \ cm
Ahora aplicamos la fórmula del área:
A = \cfrac{P\cdot a}{2} = \cfrac{13.5 \ cm \ \cdot 2.06 \ cm}{2} = 13.905\ cm^{2}
Así que el área de nuestro nonágono es 13.905 \ cm^{2}
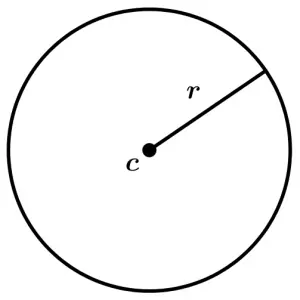
Área del círculo
El área de un círculo es igual al \pi por radio (r) al cuadrado:
A = \pi\cdot r^{2}
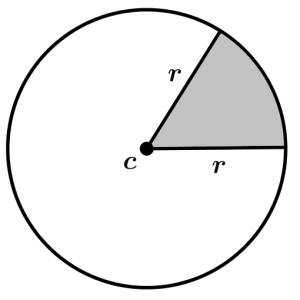
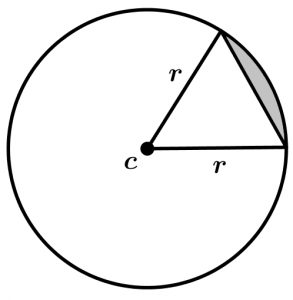
Con lo que aprendiste y un poco de sentido común ya puedes calcular el área de un sector circular y el área de un segmento circular. Las áreas sombreadas representan el sector circular y el segmento circular respectivamente:
Sector circular
Segmento circular
Verás que calcular esas áreas es más fácil de lo que parece, suerte ; )
Gracias por estar en este momento con nosotros : )
