Bienvenido de nuevo, en este ejercicio vamos a hallar la ecuación de una parábola la cual sólo tenemos el vértice y el foco.
Vamos a hallar la ecuación de la parábola que tiene de vértice el punto V(3,2) y de foco tiene el punto F(3,4).
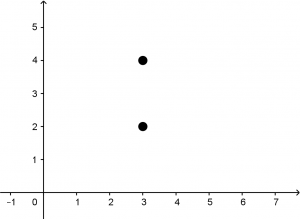
En este tipo de ejercicios es muy recomendable graficar los datos que ofrece el problema, así que en un plano cartesiano vamos a ubicar el vértice y el foco de la parábola.
V(3,2) \quad F(3,4)
Una vez que ya tengamos el foco y el vértice ubicados en el plano cartesiano, si conocemos bien las parábolas, eso quiere decir que nuestra parábola abre hacia arriba, mira la siguiente gráfica:
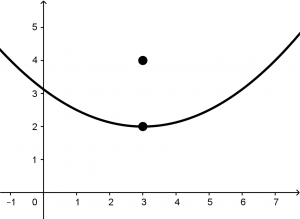 Esta parábola corresponde a la siguiente ecuación:
Esta parábola corresponde a la siguiente ecuación:
(x - x_{0})^{2} = 4p(y-y_{0})
Recordando que el vértice se representa como V(x_{0},y_{0}) y que nuestro vértice es V(3,2), vamos a sustituir estos valores en la ecuación de la parábola:
(x-3)^{2} = 4p(y-2)
¿Cómo calculamos la p de la ecuación de la parábola?
Observando que el foco es F(3,4) y que desglosando la coordenada y del foco, obtendríamos que la coordenada del foco es:
F(x_{0},y_{0} + p)
Esto ocurre porque el foco es la ubicación del vértice más la distancia p.
Como ya tenemos el valor de y_{0} que es 2 y el valor del foco que es 4, hagamos lo siguiente para poder hallar p, vamos a igualar y_{0} +p con 4:
y_{0}+p = 4
2+p = 4
p = 2
¡Ahora lo único que hay que hacer es sustituir ese valor de p en la ecuación de la parábola para obtener la ecuación de la parábola!
(x-3)^{2} = 8(y - 2)
El resultado obtenido es la forma canónica de la ecuación de la parábola.
Gracias por estar en este momento con nosotros : )