Já ouvimos a palavra “parábola”, e sim, é uma bela curva que é muito usada no dia a dia como em algumas lentes, em antenas parabólicas, em alguns túneis e às vezes para complicar um pouco a vida na escola. Portanto, vamos examinar primeiro os elementos das parábolas e, depois, os tipos de parábolas em matemática.
Elementos de uma parábola
As partes de uma parábola que iremos mencionar são as seguintes:
Vértice da parábola
O vértice da parábola é o ponto a partir do qual a parábola se abre e indica onde a parábola está localizada. Geralmente é representado pelo ponto V de vértice .
Foco da parábola
Veja o caso de uma antena parabólica, no caso prático o foco é muito importante porque todos os sinais que atingem a parábola serão recebidos no foco, não importa onde o sinal toque a antena parabólica, ele sempre alcançará o foco. Geralmente é representado como o ponto F de foco .
Distância focal da parábola
A distância focal é o longitude entre o vértice e o foco.
Lado reto da parábola
O lado reto é uma linha perpendicular à linha que une o vértice e o foco e que é quatro vezes o longitude da distância focal.
Diretriz da parábola
A diretriz é uma linha paralela com respeito ao Lado Reto e que se reflete em relação ao vértice.
Vamos resumir todas as partes da parábola mencionada no gráfico a seguir
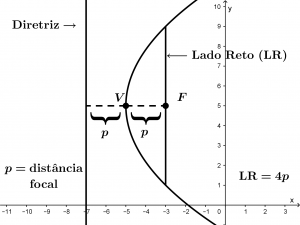
Tipos de parábolas
Vamos classificar as parábolas com relação a se eles são horizontais, verticais e se se abrem para a direita ou para a esquerda, colocaremos sua representação gráfica das parábolas e suas respectivas equações.
Parábola horizontal que se abre para a direita
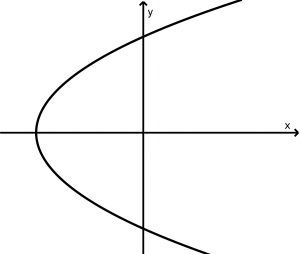
(y-y_{0})^{2} = 4p(x - x_{0})
x-(x_{0} - p) = 0
F(x_{0} + p, y_{0})
Parábola horizontal que se abre para a esquerda
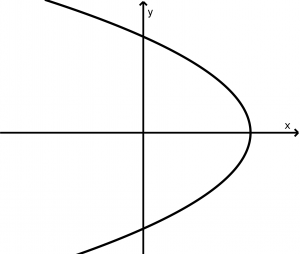
(y-y_{0})^{2} = -4p(x-x_{0})
x - (x_{0}+p) = 0
F(x_{0} \ -p, y_{0})
Parábola vertical que se abre para cima
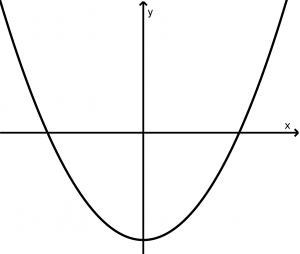
(x-x_{0})^{2} = 4p(y - y_{0})
y - (y_{0} - p ) = 0
F(x_{0}, y_{0} + p)
Parábola vertical que se abre para baixo
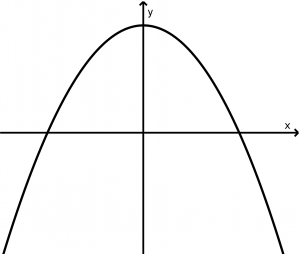
(x - x_{0})^{2} = -4p(y - y_{0})
y-(y_{0} + p )= 0
F(x_{0}, y_{0} - p)
Obrigado por estar conosco neste momento : )
