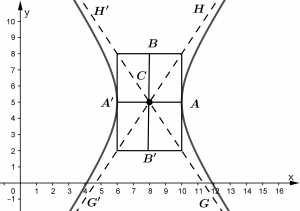
Em uma hipérbole, A e A' sempre serão usados para representar os vértices, e B e B' são usados para representar as extremidades do segmento perpendicular ao segmento \overline{AA'}. Em primeiro lugar, quero esclarecer que com um pouco de prática já será possível discernir quando a é menor ou maior que b e saber se a hipérbole se abre para cima e para baixo ou para a direita e esquerda.
Partes da hipérbole com centro em C(x_{0}, y_{0}) e segmento \overline{AA'} paralelo ao eixo x
Vamos ver nossa figura de base da hipérbole com a qual definiremos as fórmulas e os elementos da hipérbole:
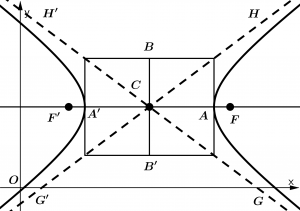
Equações da hipérbole em coordenadas retangulares:
A equação da hipérbole que se abre para a direita e para a esquerda tem a peculiaridade de que o signo da fração que contém os y será negativo:
\cfrac{(x - x_{0})^{2}}{a^{2}} - \cfrac{(y - y_{0})^{2}}{b^{2}} = 1
As coordenadas x_{0} e y_{0} sempre representam o centro C para qualquer hipérbole, não importa se é uma hipérbole que se abre para a direita e esquerda ou uma hipérbole que se abre para cima e para baixo.
- c representa o longitude do segmento \overline{CF} onde \overline{CF}=\overline{CF'}.
- a representa o longitude do segmento \overline{CA} onde \overline{CA}=\overline{CA'}.
- b representa o longitude do segmento \overline{CB} onde \overline{CB}=\overline{CB'}.
Longitude do segmento \overline{AA'}
O longitude do segmento \overline{AA'} é 2a.
Longitude do segmento \overline{BB'}
O longitude do segmento \overline{BB'} é 2b.
Longitude do centro ao foco (c)
A distância do centro C aos focos F ou F' é:
c = \sqrt{a^{2} \ + b^{2}}
Excentricidade da hipérbole
A fórmula para calcular a excentricidade da hipérbole é a seguinte:
\epsilon = \cfrac{c}{a}
A excentricidade só pode assumir valores maiores que 1: \epsilon>1, mas agora:
O que significa a excentricidade na hipérbole ou o que ela representa?
Isso significa que se o valor da excentricidade estiver próximo de 1, a hipérbole tende a ser uma linha com um segmento removido (isso acontece porque a hipérbole parece tão fechada que parece uma linha), e quanto maior o valor da excentricidade, a hipérbole tende a se assemelhar a um par de linhas paralelas.
Declive das assíntotas da hipérbole
As inclinações das assíntotas da hipérbole \overline{G'H} e \overline{GH'} são calculadas dividindo o valor do segmento vertical pelo segmento horizontal:
= \pm \cfrac{\text{segmento vertical}}{\text{segmento horizontal}}
O símbolo \pm significa que os dois signos serão usados pois a hipérbole tem duas assíntotas, o que significa que a inclinação que obtermos será positiva e negativa devido às suas duas assíntotas, daqui a pouco veremos com um exemplo.
Ponto da hipérbole em direção aos dois focos
Se P é qualquer ponto da hipérbole, PF\ -PF'=\pm 2a. O símbolo \pm depende do ramo.
Exemplo de hipérbole com centro na origem C(x_{0}, y_{0}) e com segmento \overline{AA'} paralelo ao eixo x
A equação da hipérbole é:
\cfrac{(x - 8)^{2}}{4^{2}} - \cfrac{(y - 5)^{2}}{3^{3}} = 1
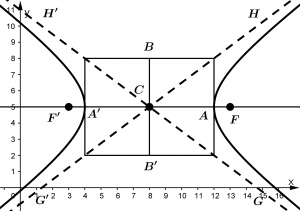
O centro da hipérbole
Como pode ser visto, o centro C da hipérbole está em:
C(8,5)
Isso significa que o centro de nossa hipérbole será encontrado nos valores que x_{0} e y_{0} têm, apenas que colocaremos os signos opostos em nossa coordenada, isso significa que como nosso valor de x_{0} é -8 e nosso valor de y_{0} é -5, então nossa coordenada do centro da hipérbole será C(8,5).
Longitude do segmento \overline{AA'}
O longitude do segmento \overline{AA'} é igual a 8, o que significa que o longitude de a é igual a 4.
Longitude do segmento \overline{BB'}
O longitude do segmento \overline{BB'} é igual a 6, o que significa que o longitude de b é igual a 3.
Distância do centro aos focos
A distância do centro C a qualquer um dos dois focos, seja F ou F', é:
c = \sqrt{4^{2} + 3^{2}} = \sqrt{16 + 9} = \sqrt{25} = 5
Portanto, o foco F está no ponto F(13,5) e o foco F' está no ponto F'(3,5).
Excentricidade da hipérbole
\epsilon = \cfrac{c}{a} = \cfrac{5}{4}=1.25
Declive das assíntotas da hipérbole
O cálculo das inclinações das assíntotas é muito simples, vamos dividir o longitude do segmento vertical pelo longitude do segmento horizontal:
\pm \cfrac{\text{segmento vertical}}{\text{segmento horizontal}} = \pm \cfrac{3}{4} = \pm 0.75
Portanto, a inclinação de uma assíntota é 0\text{.}75 e a inclinação da outra assíntota é -0\text{.}75.
Ponto da hipérbole em direção aos dois focos
Você pode fazer essa prova rapidamente tomando como P qualquer vértice da hipérbole e você verá facilmente que a fórmula PF\ -PF'=\pm 2a é demonstrada. Tente pegar o vértice (4,5).
Por que não é prático chamar os eixos da hipérbole “eixo maior” e “eixo menor”?
Simples e simplesmente porque haveria confusão ao usar as fórmulas, observe os gráficos a seguir
Gráfico da hipérbole 1
Gráfico da hipérbole 2
No gráfico da hipérbole 1 (que é o do nosso exemplo), se mencionarmos o eixo maior, tomaremos o segmento \overline{A'A}, e se mencionarmos o eixo menor, tomaremos o segmento \overline{B'B}, até agora estamos indo bem. No gráfico da hipérbole 1 (que é o do nosso exemplo), se mencionarmos o eixo maior, tomaremos o segmento \overline{A'A}, e se mencionarmos o eixo menor, tomaremos o segmento \overline{B'B}, até agora estamos indo bem.
Se estiver estudando as fórmulas, você deseja determinar as inclinações das linhas assintóticas do Gráfico da hipérbole 2 e aprendeu a fórmula da seguinte maneira:
\pm \cfrac{\text{eixo menor}}{\text{eixo maior}}
Você notará que agora o eixo menor é horizontal e o eixo maior é vertical, o que significa que a inclinação obtida não resultará na inclinação de suas assíntotas de seu Gráfico da Hipérbole 2. Portanto, para encontrar a inclinação das assíntotas da hipérbole, vamos nos acostumar a chamar os eixos de “segmento vertical” e “segmento horizontal”.
\pm \cfrac{\text{segmento vertical } }{\text{segmento horizontal}}
Hipérbole com centro em C(x_{0}, y_{0}) e segmento \overline{AA'} paralelo ao eixo y
Veja o seguinte exemplo:
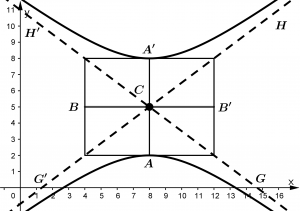
Qual sua equação é:
\cfrac{(y - 5)^{2}}{3^{2}} - \cfrac{(x - 8)^{2}}{4^{2}} = 1
Quando a hipérbole se abre para cima e para baixo, o denominador da fração que tem y ‘s agora será a e o denominador da fração que tem x‘s agora será b. O que significa que a equação para as hipérboles que se abrem para cima e para baixo é:
\cfrac{(y - y_{0})^{2}}{a^{2}} - \cfrac{(x - x_{0})^{2}}{b^{2}} = 1
Diz-se que a segue o signo positivo e b segue o signo negativo, mas todas as fórmulas acima são usadas exatamente da mesma forma.
Obrigado por estar conosco neste momento :)