Um ângulo é a abertura formada por duas retas, semi-retas ou segmentos que compartilham um ponto comum denominado vértice e de acordo com sua medida e seu agrupamento, podemos classificar os ângulos de duas maneiras diferentes.
Agora veremos os tipos de ângulos de acordo com sua medida e de acordo com seu agrupamento.
Classificação dos ângulos de acordo com sua medida
Ângulo agudo
O ângulo agudo é aquele que mede mais de 0° e menos de 90°.
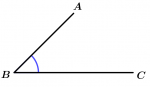
0° < \ \measuredangle ABC < 90°
\measuredangle ABC \ \text{ é agudo}
Ângulo reto
O ângulo reto é aquele que mede 90° e geralmente é simbolizado por um pequeno quadrado no vértice do ângulo.
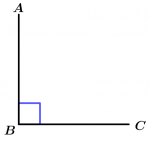
\measuredangle ABC = 90°
\measuredangle ABC \ \text{ é o ângulo reto}
Ângulo obtuso
O ângulo obtuso é o ângulo que mede mais de 90° e menos de 180°.
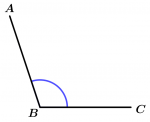
90° < \measuredangle ABC < 180°
\measuredangle ABC \ \text{ é obtuso}
Ângulo plano ou ângulo raso
O ângulo raso é aquele que mede exatamente 180°.
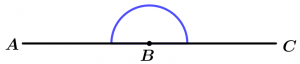
\measuredangle ABC = 180°
\measuredangle ABC \ \text{ é raso }
Ângulo de entrada
O ângulo de entrada é aquele que mede mais de 180° e menos de 360 °.
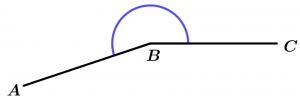
180° < \measuredangle ABC < 360°
\measuredangle ABC \ \text{ é ângulo de entrada}
Ângulo perigonal ou ângulo giro ou ângulo completo
O ângulo perigonal mede exatamente 360°.
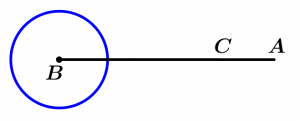
\measuredangle ABC= 360°
\measuredangle ABC \ \text{ é completo}
Classificação dos ângulos de acordo com seu agrupamento
Ângulos adjacentes
Os ângulos adjacentes são dois ângulos que têm um lado e um vértice em comum.
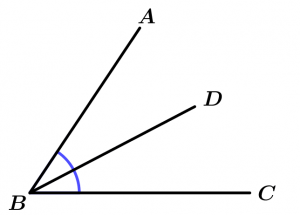
\measuredangle ABD \ \text{ é adjacente a } \ \measuredangle DBC
Ângulos opostos pelo vértice
Os ângulos opostos pelo vértice são aqueles em que os lados de um ângulo são o prolongamento dos lados de outro ângulo e também são congruentes.
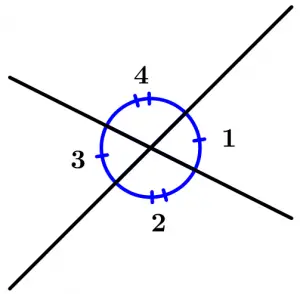
\measuredangle 1 \ \text{ é oposto a } \ \measuredangle 3 \ \text{ e } \ \measuredangle 1 \cong \measuredangle 3
\measuredangle 4 \ \text{ é oposto a } \ \measuredangle 2 \ \text{ e } \ \measuredangle 4 \cong \measuredangle 2
Ângulos complementares
Ângulos complementares são dois ângulos cujas medidas somam 90° e podem ou não ser adjacentes.
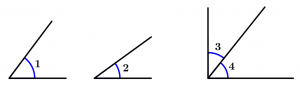
\measuredangle 1 + \measuredangle 2 = 90°
\measuredangle 3 + \measuredangle 4 = 90°
\measuredangle 1 \ \text{ e } \ \measuredangle 2 \ \text{ não são adjacentes e }
\measuredangle 3 \ \text{ e } \ \measuredangle 4 \ \text{ são adjacentes }
Ângulos suplementares
Los ángulos suplementarios son dos ángulos cuyas medidas sumadas dan como resultado 180° y pueden ser adyacentes o no.
\measuredangle 1 + \measuredangle 2 = 180°
\measuredangle 3 + \measuredangle 4 = 180°
\measuredangle 1 \ \text{ e } \ \measuredangle 2 \ \text{ não são adjacentes e }
\measuredangle 3 \ \text{ e } \ \measuredangle 4 \ \text{ são adjacentes }
Ângulos conjugados
Os ângulos conjugados são dois ângulos cujas medidas somadas dão 360° e podem ou não ser adjacentes.
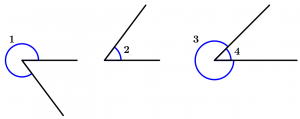
\measuredangle 1 + \measuredangle 2 = 360°
\measuredangle 3 + \measuredangle 4 = 360°
\measuredangle 1 \ \text{ e } \ \measuredangle 2 \ \text{ não são adjacentes e }
\measuredangle 3 \ \text{ e } \ \measuredangle 4 \ \text{ são adjacentes }
Obrigado por estar conosco neste momento : )
