Alguna vez han oído la palabra «parábola», es una bella curva la cual utilizáis mucho en la vida cotidiana como en algunos lentes, en las antenas parabólicas, en túneles y a veces para complicar un poco la existencia en la escuela. Así que primero os vamos a mostrar los elementos de las parábolas y luego os vamos a enseñar los tipos de parábolas en matemáticas.
Elementos de una parábola
Las partes de una parábola que os mencionamos son las siguientes:
Vértice de la parábola
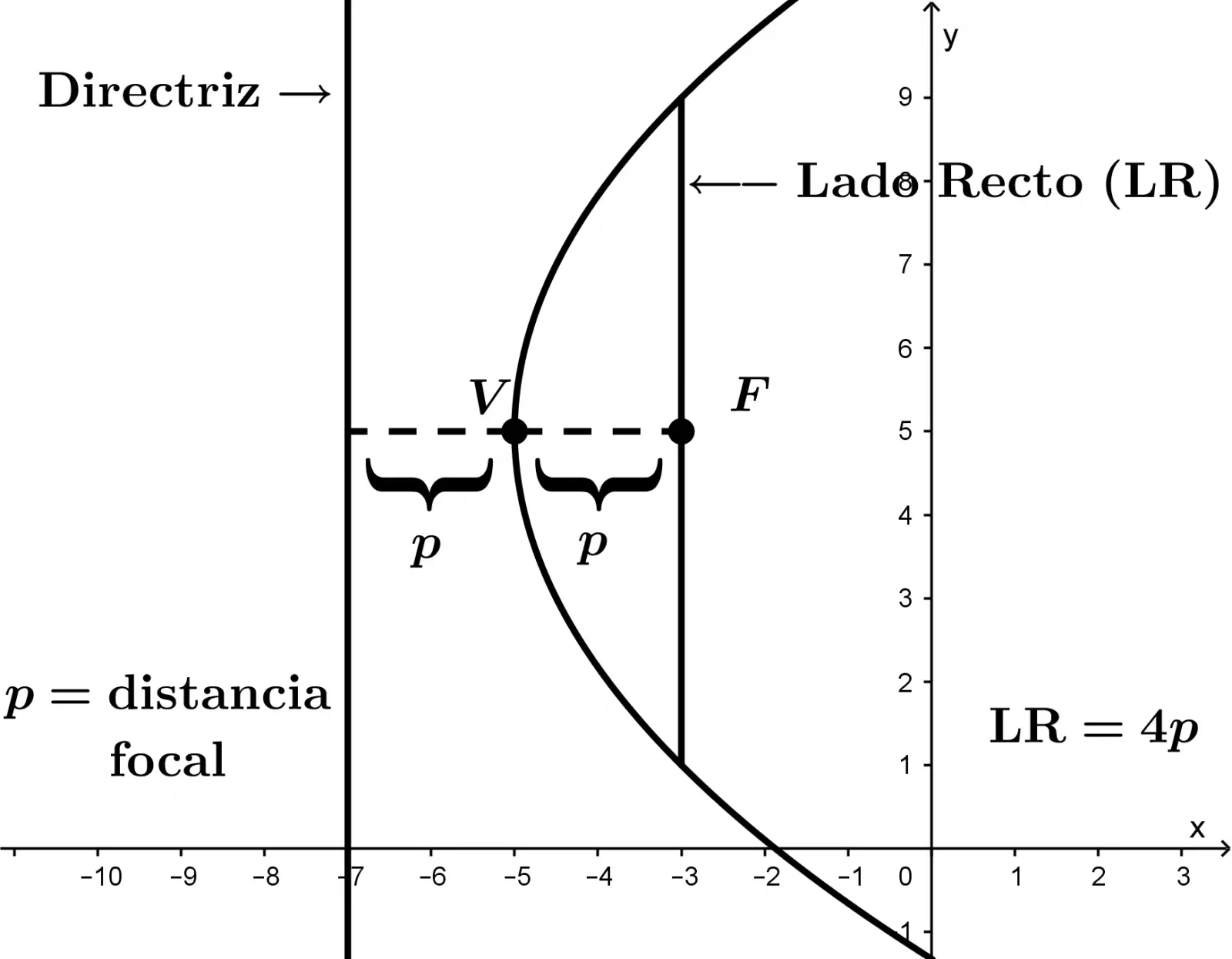
El vértice de la parábola es el punto a partir del cual abre la parábola, e indica en dónde está localizada la parábola. Os la representamos con el punto V de vértice.
Foco de la parábola
Tomemos el caso de una antena parabólica, en el caso práctico el foco es muy importante porque todas las señales que lleguen a la parábola serán recibidas en el foco, no importa el punto que la señal toque la antena parabólica, siempre llegará al foco. La representamos como el punto F de foco.
Distancia focal de la parábola
La distancia focal es la longitud que hay entre el vértice y el foco.
Lado recto de la parábola
El lado recto es una línea perpendicular a la línea que une el vértice y el foco y que tiene cuatro veces la longitud de la distancia focal.
Directriz de la parábola
La directriz es una línea paralela con respecto al Lado Recto y la encontramos reflejada con respecto al vértice.
Os vamos a resumir todas las partes de la parábola en la siguiente imagen
Tipos de parábolas
Os vamos a clasificar a las parábolas con respecto si son horizontales, verticales y si abren hacia la derecha o a la izquierda, os colocaremos su representación gráfica de las parábolas y sus respectivas ecuaciones.
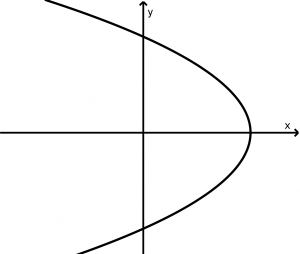
Parábola horizontal que abre hacia la derecha
(y-y_{0})^{2} = 4p(x - x_{0})
x-(x_{0} - p) = 0
F(x_{0} + p, y_{0})
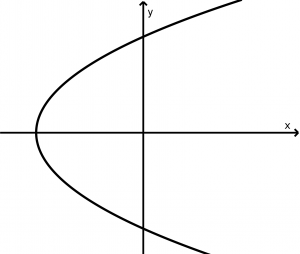
Parábola horizontal que abre hacia la izquierda
(y-y_{0})^{2} = -4p(x-x_{0})
x - (x_{0}+p) = 0
F(x_{0} \ -p, y_{0})
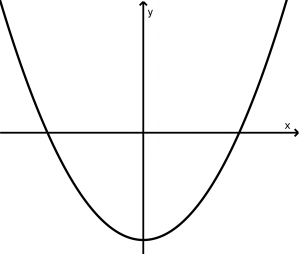
Parábola vertical que abre hacia arriba
(x-x_{0})^{2} = 4p(y - y_{0})
y - (y_{0} - p ) = 0
F(x_{0}, y_{0} + p)
Parábola vertical que abre hacia abajo
(x - x_{0})^{2} = -4p(y - y_{0})
y-(y_{0} + p )= 0
F(x_{0}, y_{0} - p)
Os agradecemos por estar en este instante con nosotros : )