Trigonometric identities 📐

The most common trigonometric identities

1. \quad \sin^{2}x+\cos^{2}x=1
2. \quad \tan^{2}x+1=\sec^{2}x
3. \quad \cot^{2}x+1=\csc^{2}x
4. \quad \sin x \csc x =1
5. \quad \cos x \sec x= 1
6. \quad \tan x \cot x =1

Identities quotients

7. \quad \tan x=\cfrac{\sin x}{\cos x}
8. \quad \cot x=\cfrac{\cos x}{\sin x}=\cfrac{1}{\tan x}

Power reduction formulas

9. \quad \sin^{2}x=\cfrac{1}{2}-\cfrac{1}{2}\cos 2x
10. \quad \cos^{2}x=\cfrac{1}{2}+\cfrac{1}{2}\cos 2x
11. \quad \tan^{2}x = \cfrac{1 - \cos\left(2x\right)}{1 + \cos\left(2x\right)}
12. \quad \sin^{2}\left(\cfrac{x}{2}\right)=\cfrac{1}{2}-\cfrac{\cos x}{2}
13. \quad \cos^{2}\left(\cfrac{x}{2}\right)=\cfrac{1}{2}+\cfrac{\cos x}{2}
14. \quad \sin^{3} x = \cfrac{3}{4} \sin x - \cfrac{1}{4} \sin 3x
15. \quad \cos^{3}x = \cfrac{3}{4} \cos x + \cfrac{1}{4} \cos 3x
16. \quad \sin^{4}x = \cfrac{3}{8} - \cfrac{1}{2} \cos 2x + \cfrac{1}{8} \cos 4x
17. \quad \cos^{4}x = \cfrac{3}{8} + \cfrac{1}{2} \cos 2x + \cfrac{1}{8} \cos 4x
18. \quad \sin^{5}x = \cfrac{5}{8} \sin x - \cfrac{5}{16} \sin 3x + \cfrac{1}{16} \sin 5x
19. \quad \cos^{5}x = \cfrac{5}{8} \cos x + \cfrac{5}{16} \cos 3x + \cfrac{1}{16} \cos 5x

Odd pair trigonometric identities

20. \quad \sin(-x)=-\sin x
21. \quad \cos(-x)=\cos x
22. \quad \tan(-x)=-\tan x
23. \quad \cot(-x)=-\cot x
24. \quad \sec(-x)= \sec x
25. \quad \csc(-x)= -\csc x

Co-function identities

26. \quad \sin\left(\cfrac{\pi}{2}-x\right)=\cos x
27. \quad \cos\left(\cfrac{\pi}{2}-x\right)=\sin x
28. \quad \tan\left(\cfrac{\pi}{2}-x\right)=\cot x
29. \quad \csc\left(\cfrac{\pi}{2} - x \right) = \sec x
30. \quad \sec \left( \cfrac{\pi}{2} - x \right) = \csc x
31. \quad \cot \left(\cfrac{\pi}{2} - x \right) = \tan x

Addition and subtraction of angles of trigonometric functions

32. \quad \sin(x+y)= \sin x \cos y +\cos x \sin y
33. \quad \sin(x-y)= \sin x \cos y - \cos x \sin y
34. \quad \cos(x+y)= \cos x \cos y - \sin x \sin y
35. \quad \cos(x-y) = \cos x \cos y + \sin x \sin y
36. \quad \tan(x+y) = \cfrac{\tan x + \tan y}{1 - \tan x \tan y}
37. \quad \tan(x-y) = \cfrac{\tan x - \tan y}{1 + \tan x \tan y}
38. \quad \cot(x+y) = \cfrac{\cot x \cot y - 1}{\cot x + \cot y}
39. \quad \cot(x-y) = \cfrac{\cot x \cot y + 1}{\cot x - \cot y }

Average angles of trigonometric functions

40. \quad \sin \left(\cfrac{x}{2}\right) = \sqrt{\cfrac{1-\cos x}{2}}
41. \quad \cos \left(\cfrac{x}{2}\right) = \sqrt{\cfrac{1+\cos x}{2}}
42. \quad \tan \left(\cfrac{x}{2}\right)= \sqrt{\cfrac{1-\cos x}{1+\cos x}}= \cfrac{1- \cos x}{\sin x}= \cfrac{\sin x}{1 + \cos x}
43. \quad \cot \left(\cfrac{x}{2}\right)= \sqrt{\cfrac{1 + \cos x}{1 - \cos x}}= \cfrac{\sin x}{1 -\cos x}= \cfrac{1 + \cos x}{\sin x}

Formulas of the double of an Angle of the trigonometric functions

44. \quad \sin 2x = 2 \sin x \cos x
45. \quad \cos 2x = \cos^{2} x - \sin^{2} x = 2 \cos^{2} x - 1
46. \quad \tan 2x=\cfrac{2 \tan  x}{1-\tan^{2} x}

Multiple angle formulas of trigonometric functions

47. \quad \sin 3x = 3 \sin x-4 \sin^{3} x
48. \quad \cos 3x = 4 \cos^{3} x- 3 \cos x
49. \quad \tan 3x = \cfrac{3 \tan x - \tan^{3} x}{1-3\tan^{2} x}
50. \quad \sin 4x = 4 \sin x \cos x - 8 \sin^{3} x \cos x
51. \quad \cos 4x = 8 \cos^{4} x -8 \cos^{2} x + 1
52. \quad \tan 4x = \cfrac{4 \tan x - 4 \tan^{3} x}{1-6 \tan^{2} x + \tan^{4} x}
53. \quad \sin 5x = 5 \sin x-20 \sin^{3} x + 16 \sin^{5} x
54. \quad \cos 5x = 16 \cos^{5} x-20 \cos^{3} x+5 \cos x
55. \quad \tan 5x = \cfrac{\tan^{5} x - 10 \tan^{3} x + 5 \tan x}{1-10 \tan^{2} x + 5 \tan^{4} x}

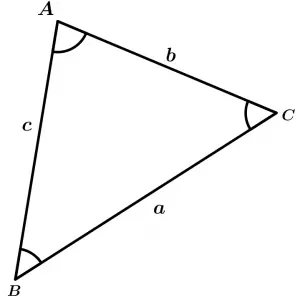
Relations between the sides and angles of a flat triangle

Law of sines

56. \quad \cfrac{a}{\sin A} = \cfrac{b}{\sin B} = \cfrac{c}{\sin C}

Law of cosines

57. \quad c^{2} = a^{2} + b^{2} - 2ab \cos C

Law of tangents

58. \quad \cfrac{a + b}{a - b} = \cfrac{\tan\frac{1}{2}(A + B)}{\tan\frac{1}{2}(A - B)}

Sum, difference and product of trigonometric functions

Sine of A plus sine of B

59. \quad \sin A + \sin B = 2 \sin \frac{1}{2}(A + B) \cos \frac{1}{2}(A - B)

Sine of A minus sine of B

60. \quad \sin A - \sin B = 2 \cos \frac{1}{2}(A + B) \sin \frac{1}{2}(A - B)

Cosine of A plus cosine of B

61. \quad \cos A + \cos B = 2 \cos \frac{1}{2}(A + B) \cos \frac{1}{2}(A - B)

Cosine of A minus cosine of B

62. \quad \cos A - \cos B = 2 \sin \frac{1}{2}(A + B) \sin \frac{1}{2}(B - A)

Sine of A by sine of B

63. \quad \sin A \sin B = \frac{1}{2} \{ \cos(A - B) - \cos(A + B)\}

Cosine of A by cosine of B

64. \quad \cos A \cos B = \frac{1}{2} \{ \cos(A - B) + \cos(A + B)\}

Sine of A by cosine of B

65. \quad \sin A \cos B = \frac{1}{2} \{ \sin(A - B) + \sin(A + B)\}

Thank you for being at this moment with us :)