A continuación veremos varios ejercicios de instalaciones eléctricas sencillos, aclaro que no son ejercicios de circuitos eléctricos como tal, son ejercicios como si fuéramos a realizar una instalación eléctrica en un edificio, no como si fuéramos a realizar alguna placa fenólica con varios circuitos más complejos.
Ejercicio 1 de instalaciones eléctricas
Tenemos el siguiente circuito que alimenta una lámpara y el objetivo de este ejercicio es encontrar la resistencia que se opone al paso de la corriente.
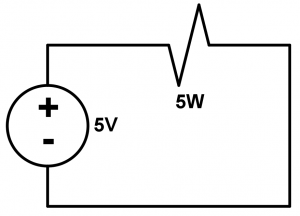
Este ejercicio es muy sencillo, es puro formulazo el que haremos, utilizando la siguiente fórmula se resuelve el ejercicio:
P=\cfrac{V^{2}}{R}
Y lo único que tenemos qué hacer es despejar la resistencia:
R=\cfrac{V^{2}}{P}
Ahora simplemente aplicamos variables que ya tenemos como el voltaje de 5V y la potencia de la lámpara de 5W:
R=\cfrac{(5V)^{2}}{5W} = 5 \Omega
Eso nos da como resultado que la resistencia de nuestra lámpara es de 5\Omega
Ejercicio 2 de instalaciones eléctricas
Una lámpara tiene una resistencia de 181.1\Omega y se conecta al voltaje de una vivienda. Tomando el voltaje promedio o común de 127V y utilizando el siguiente circuito, ¿cuál es la potencia de la lámpara?
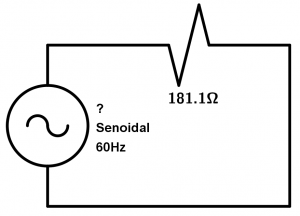
Para este ejercicio utilizaremos la fórmula del ejercicio 1 y aplicamos directamente la fórmula:
P=\cfrac{(127V)^{2}}{181.1\Omega }=89.06W
Así que la potencia de nuestra lámpara es de 89.06W
Ten en cuenta que en este ejercicio nos dieron otros datos como la frecuencia y que es una senoidal. En este tipo de ejercicios no nos afecta en nada que sea de una frecuencia de 50\text{Hz} o 60\text{Hz}, si ya nos están comentando que el voltaje es de 127V, es más que suficiente para nosotros para poder resolver el ejercicio.
Te lo comento para que no te me vayas a estresar porque como ven que en un ejercicio te dan más datos quiere decir que los tienes que utilizar.
Ejercicio 3 de instalaciones eléctricas
En un circuito en serie con voltaje de 127V y resistencias mostradas en el circuito, calcular la resistencia total R_{T} , la intensidad I y la potencia P.
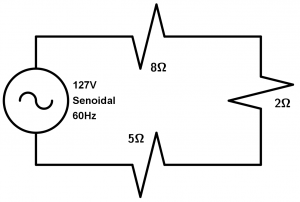
Comencemos con la resistencia total, simplemente es una suma ya que están todas las resistencias en serie, entonces para nuestra resistencia equivalente tenemos lo siguiente:
R_{T} = 8\Omega + 2\Omega + 5\Omega \ \rightarrow R_{T} = 15 \Omega
Así que tenemos que nuestra resistencia total es igual a 15\Omega
Para la intensidad nada mas aplicaremos una simple fórmula de la Ley de Ohm:
I = \cfrac{V}{R} = \cfrac{127V}{15\Omega} = 8.46A
La intensidad del circuito es de 8.46A
Y para la potencia aplicamos una fórmula con el voltaje y la intensidad que ya tenemos y que ya calculamos:
P =127V \times 8.46A = 1074.42W
Entonces nuestra potencia es de 1074.42W
Ejercicio 4 de instalaciones eléctricas
Calcula la corriente total que circulará en el circuito y las tensiones de cada resistencia. Al final comprueba el voltaje total sumando los voltajes de todas las resistencias.
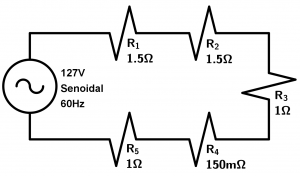
Como hicimos en el ejercicio anterior, como tenemos que todas las resistencias están en serie, simplemente tenemos que sumarlas:
R_{T} = R_{1} + R_{2} + R_{3} + R_{4} + R_{5}
R_{T} = 1.5\Omega + 1.5 \Omega + 1 \Omega + 1 \Omega + 0.15\Omega
La suma nos da una resistencia equivalente de 5.15\Omega
Seguidamente lo que tenemos qué hacer es aplicar la fórmula de Ley de Ohm para obtener la corriente total del circuito:
I_{T} = \cfrac{127V}{5.15\Omega} = 24.66A
Así que tenemos que la corriente total del circuito es de 24.66A.
En este último paso de calcular los voltajes de cada resistencia simplemente tendremos qué hacer varias multiplicaciones con la misma fórmula de la Ley de Ohm de V = R \times I
V_{R1} = 1.5\Omega \times 24.66A = 36.99V
V_{R2} = 1.5\Omega \times 24.66A = 36.99V
V_{R3} = 1\Omega \times 24.66A = 24.66V
V_{R4} = 0.15\Omega \times 24.66A = 3.69V
V_{R5} = 1\Omega \times 24.66A = 24.66V
Al realizar todas las sumas de las resistencias, tenemos lo siguiente:
36.99V+36.99V+24.66V+3.69V+24.66V = 126.99V
Ejercicio 5 de instalaciones eléctricas
Calcule la corriente total que circulará por el circuito y la resistencia total del mismo. Recuerda que la resistencia total del circuito debe ser menor que las resistencias parciales.
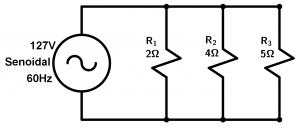
Para empezar la fórmula que utilizaremos es la de la suma de las resistencias en paralelo, la puedes ver dando click aquí. Así que vamos a empezar:
\cfrac{1}{R_{T}} = \cfrac{1}{2} + \cfrac{1}{4} + \cfrac{1}{5} = \cfrac{10}{20} + \cfrac{5}{20} + \cfrac{4}{20} = \cfrac{19}{20}
Ahora que tenemos el total, tenemos que despejar para hallar nuestra resistencia equivalente del circuito en paralelo:
\cfrac{1}{R_{T}} = \cfrac{19}{20} \ \rightarrow \ R_{T} = \cfrac{20}{19} = 1.05\Omega
Así que nuestra resistencia equivalente es igual a 1.05\Omega.
Y simplemente para calcular la intensidad de nuestra fuente, aplicamos la fórmula de la Ley de Ohm con la intensidad despejada:
I=\cfrac{127V}{1.05\Omega} = 120.95A
Finalmente tenemos que nuestra corriente del circuito es de 120.95A.
Ejercicio 6 de instalaciones eléctricas
Calcule la resistencia total del circuito, la corriente total y la potencia que circulará. Compruebe calculando las corrientes parciales y sumándolas.
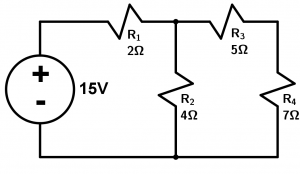
Para empezar con este ejercicio, lo que haremos es sumar la resistencia 3 con la 4 debido a que están en serie, lo que nos da un valor de 12\Omega.
Seguidamente tenemos que calcular la resistencia equivalente de los 12\Omega con la resistencia 2 sumando en paralelo:
\cfrac{1}{R_{T}} = \cfrac{1}{12} + \cfrac{1}{4} = \cfrac{1}{12} + \cfrac{3}{12} = \cfrac{4}{12} =\cfrac{1}{3} \rightarrow R_{2,3,4} = 3\Omega
Ahora tenemos que sumar la resistencia equivalente con la resistencia 1, como están en serie, tendremos una resistencia total de 5\Omega.
La corriente simplemente se calcula con la Ley de Ohm:
I=\cfrac{V}{R} = \cfrac{15V}{5\Omega}=3A
Así que nuestra corriente es de 3A.
Calculamos el voltaje de la resistencia 1:
V_{R1} = 2\Omega \times 3A = 6V
El voltaje de las resistencias 2, 3 y 4 es la diferencia del total con el calculado, eso quiere decir que es 9V. Dándonos a entender que el voltaje en la resistencia 2 es de 9V y el voltaje en la resistencia equivalente de 3 y 4 también es de 9V.
Como ya tenemos los voltajes, simplemente tenemos que hallar las corrientes que circularán en la resistencia 2 y en la resistencia equivalente de 3 y 4. Simplemente utilizamos Ley de Ohm:
I_{R2} = \cfrac{9V}{4\Omega } = 2.25A \qquad I_{R3,4} = \cfrac{9V}{12\Omega} 0.75A
Sumando estas dos resistencias obtenemos un valor de 3A, dándonos el mismo valor que de la corriente total del circuito, lo que quiere decir que son correctos los cálculos tanto de resistencias equivalentes como de las corriente que circulan en determinadas resistencias.
Gracias por estar en este momento con nosotros : )
