Aquí hablaremos de las cosas más relevantes que nos interesan saber del Cubo Rubik, no nos andaremos con rollos.
El cubo de rubik o Rubik´s Cube es un cubo de colores el cual lo inventó el arquitecto y profesor húngaro Ernő Rubik (ver imagen 1) en 1974. El cual lo había creado en un principio para ayudar a sus alumnos a demostrar unos conceptos de geometría, Ernő, al desordenarlo e intentar volver a ordenarlo, se dio cuenta de que era complejo, lo que marcó el inicio de una nueva era de rompecabezas que hoy en día se realizan competencias en todo el mundo.

Cómo armar la última capa del cubo de rubik
Lo que uno recomienda desde un principio es que si quiere practicar velocidad, se aprenda de una vez los 57 algoritmos del OLL y los 21 algoritmos del PLL, pero sino, les dejamos aquí varias opciones para resolver la última capa del cubo de Rubik.
Nos detendremos a ver unos algoritmos para resolver la última capa del cubo de rubik, el proceso que conlleva resolver las primeras dos capas no las veremos aquí.
Cuando llegamos a la última capa lo que haremos primero es resolver la cara amarilla y después resolveremos con permutaciones los colores de alrededor de la última capa. Primero será hacer una cruz, luego giraremos todas las esquinas para que la cara sea de un sólo color y después acomodaremos todas las piezas con permutaciones para finalmente tener el cubo armado.
Cuando lleguemos a la última capa, si no tuvimos la suerte de que tengamos la cruz armada, tendremos que armarla, y para eso tenemos los siguientes casos y sus resoluciones (ver figuras 2, 3, 4 y 5):
 | F U R U’ R’ F’ |
 | F R U R’ U’ F’ |
 | F U R U’ R’ F’ U F R U R’ U’ F’ |
 | NADA |
Una vez que ya tenemos la cruz formada, sólo nos queda acomodar las esquinas para que esté completa la cara de la última capa. Para hace tenemos dos opciones, una es aplicar un algoritmo que acomoda de esquina en esquina y la otra opción que es mucho más recomendable que la primera es aprenderse unos cuantos algoritmos.
Primera opción para completar la cara de la última capa del cubo de rubik
Para la primera opción, lo que haremos es tener una esquina base (ver figura 6), en la cual iremos acomodando esquina por esquina.

Entonces aplicaremos el siguiente algoritmo:
R’ D’ R D
Lo hacemos las veces que sean necesarias hasta que la esquina base sea del color de las demás, en este caso es amarillo (ver figura 7).

Luego sólo giramos la capa amarilla para colocar una esquina desacomodada en nuestra esquina base (ver figura 8).
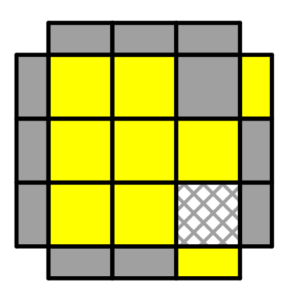
Y repetimos el mismo procedimiento de aplicar el algoritmo R’ D’ R D hasta que se acomode la esquina y luego colocamos la última esquina desacomodada en la esquina base y volvemos a aplicar el algoritmo y ¡listo!
Segunda opción para completar la cara de la última capa del cubo de rubik
Simple y sencillamente es aprenderse los algoritmos que se muestran a continuación:
 | R U2’ R2’ U’ R2 U’ R2’ U2’ R |  | R U R’ U R U’ R’ U R U2’ R’ |
 | R U2’ R’ U’ R U’ R’ |  | R U R’ U R U2’ R’ |
 | r U R’ U’ r’ F R F’ |  | R2 D R’ U2 R D’ R’ U2 R’ |
 | F’ r U R’ U’ r’ F R |
Esta segunda opción es la más recomendable porque tus tiempos disminuirán mucho y además ya tendrás aprendidos 7 algoritmos de los demás casos de OLL. Recuerda que son 57 algoritmos, por lo que sólo te faltarían 50.
Ahora que ya tienes la cara de la última capa resuelta, sólo nos queda permutar.
Permutar la última capa del cubo de rubik
Para permutar la última capa hay varias opciones, pero sólo vamos a mostrar las dos que más recomendamos. La primera opción va a ser la de aprenderse 2 algoritmos del PLL, uno para permutar esquinas y el otro para permutar aristas; y la segunda opción va a ser aprenderse todos los algoritmos del PLL. Así, que si empiezas con la primera opción almenos ya tendrás avanzado dos algoritmos del PLL, recuerda que son 21, nada más te faltarían 19.
Primera opción para permutar la última capa del cubo de rubik
A continuación mostraremos 2 algoritmos, 1 se llama la permutación tipo T que lo utilizaremos para permutar las esquinas y el otro algoritmo es una permutación tipo U, que nos servirá para permutar aristas.
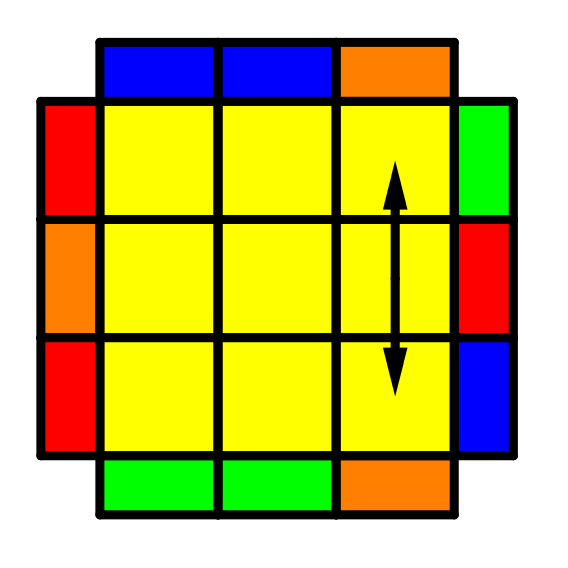 | R U R’ U’ R’ F R2 U’ R’ U’ R U R’ F’ |  | R U’ R U R U R U’ R’ U’ R2 |
Con la permutación tipo T lo que vas a hacer es acomodar las esquinas y una vez que ya las tengas acomodadas, utilizarás la permutación tipo U para acomodar las aristas, sólo te dejaré de tarea que apliques la permutación tipo U las veces que sean necesarias y que le pongas un poco de cabeza para que te des más idea de cómo funciona el cubo de rubik para que lo puedas resolver y te asombres más.
Segunda opción para permutar la última capa del cubo de rubik
La segunda opción y es la más recomendable ya que no son muchos los algoritmos para aprenderse, es de una vez estudiar los 21 algoritmos del PLL, te los dejo aquí para que les des un vistazo.
¡Ya con toda la información que tienes en este post estás listo para resolver la última capa del cubo de Rubik!
Gracias por estar en este momento con nosotros : )
