A solid of revolution is generated by rotating around the axis y, the region bounded by the curve y=\sqrt[3]{x}, the axis x and the line x = c where c > 0. Calculate the value of c so that the solid has a volume of 12\pi u^{3}. The u^{3} means cubic units.
To find the volume of the solid of revolution, we will use the method of cylindrical shells.
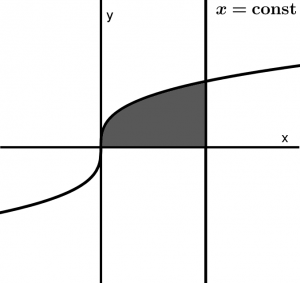
Let’s graph the function of y=\sqrt[3]{x} and put the line x=c
We are going to write the equation with which we will find the value of c, what we will do is write an integral and we will match it to the volume value of 12\pi u^{3} that the exercise tells us, the limits of the integral must be from zero to the value of c:
\displaystyle V = \int_{0}^{c}2\pi x\sqrt[3]{x} = 12 \pi
By properties of the integrals we will extract the constants of the integral and reduce the x‘s:
\displaystyle 2\pi \int_{0}^{c} x^{\frac{4}{3}} = 12 \pi
We cancel terms and perform the integral of x^{\frac{4}{3}} which, by chain rule, equals \frac{3}{7}x^{\frac{7}{3}}:
\cancel{2}\cancel{\pi} \int_{0}^{2} x^{\frac{4}{3}} = \cancel{12} \cancel{\pi}
\left. \cfrac{3x^{\frac{7}{3}}}{7}\right]_{0}^{c} = 6
We evaluate, multiply by 7 and divide by 3 all equality:
\cfrac{3c^{\frac{7}{3}}}{7} = 6
c^{\frac{7}{3}} = 14
Next we will raise all the equality to the cube to eliminate the denominator 3 of the power of \frac{7}{3}:
c^{7} = 14^{3} = 2744
Now we will apply the root to the 7 to all the equality to obtain the value of c:
c = \sqrt[7]{2744} \approx 3.098
So our value of c for the volume to be 12\pi u^{3}, must have a value of \sqrt[7]{2744}.
Thank you for being at this moment with us : )