Interval Definition
The subset of real numbers comprised between any two of its elements is called an interval: a and b; which are called extremes of the interval.
Geometrically, the intervals correspond to line segments, rays or the same real line.
Closed interval
It is the set of real numbers formed by a, b and all the elements between them. That is, it is that interval whose ends belong to the given interval and is represented by brackets [ ].
[a,b] = \{ x / a \le x \le b \}
With respect to graphical notation, it is denoted by filled circles, denoted as closed. That is, as shown in the following image:

Open interval
It is the set of real numbers between a and b. That is to say, it is that interval whose extremes are not contained in the interval, they only serve as borders. To represent this range, parentheses ( ) are used.
(a,b) = \{ x / a < x < b \}
With respect to graphical notation, it is denoted by empty circles, denoted as open. That is, as shown in the following graph:

Semi-open or semi-closed interval
It is that interval that does not contain one of the extremes, it can be located to the right or left. It is represented by combining parentheses and brackets: ( ] or [ ). Namely:
Interval half-open to the left (or half-closed to the right)
(a,b] = \{ x / a < x \le b \}

Interval half-open to the right (or half-closed to the left)
[a,b) = \{ x / a \le x < b \}

Infinite interval
It is that interval that has at least one of its ends at infinity \infty. Infinity, being an immeasurable quantity (not measurable), uses parentheses for its representation.
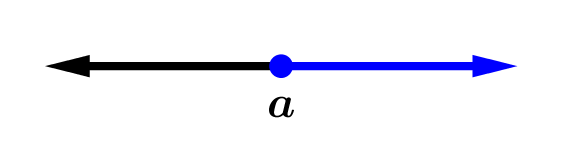 | 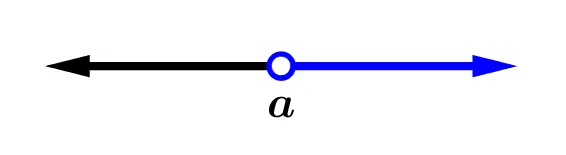 |
| [a,+\infty) = \{x / x \ge a \} | (a,+\infty)=\{ x / x > a \} |
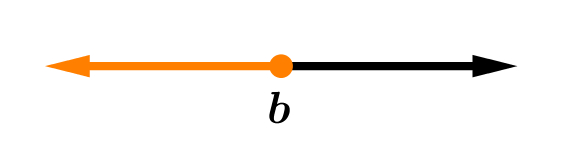 | 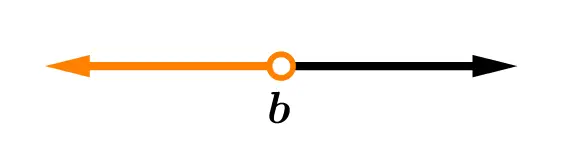 |
| (-\infty, b] = \{ x / x \le b \} | (-\infty,b) = \{x / x < b \} |
| (-\infty,+\infty) = \mathbb{R} |  |
Thank you for being in this moment with us : )
