▷ Area Between Functions

In this post we will learn how to calculate the area of a function with absolute value. It is much easier than it seems.

Let’s start

For the function $f(x)=|x^{3}-x|$ calculate the area under the curve that is between the limits of $x = -1$ and $x = 1$ .

You have to have a bit of skill with this function, remember that we want to calculate the area of the function $f(x)$ , but decompose $f(x)$ in two functions as: 1. $x^{3} - x$ and 2. $x - x^{3}$ is not enough if you do not know how they behave.

Let’s calculate the intersection points of the function $f(x)$ . It must be equal to zero:

$x^{3} - x = 0$

We will factor a single $x$ :

$x(x^{2} - 1) = 0$

Now we will factor the binomial:

$x(x + 1)(x - 1) = 0$

And what we can observe is that the points of intersection are when $x=-1$ , $x=0$ and $x=1$ , with this we can even raise our integral, only missing a few more things.

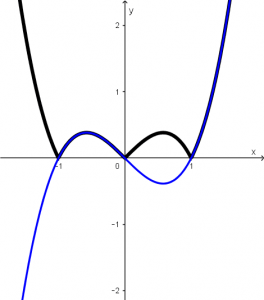
By decomposing the function $f(x)$ , the first function obtained that is $x^{3}-x$ is painted blue and it will be visualized in the following way:

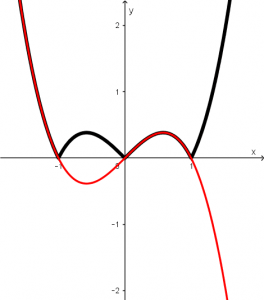
And the second function obtained that is $x- x^{3}$ is painted red and will be displayed as follows:

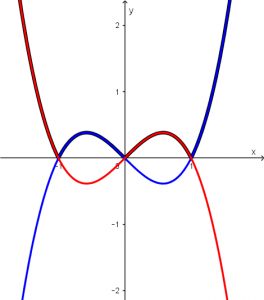
If we join the two functions in the same graph we will obtain the following:

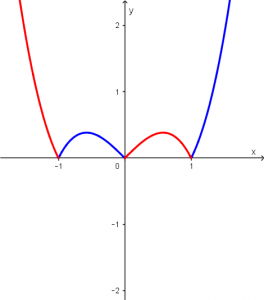
Okay, but from what you see, we do not need the whole function, we need a part of each of the functions. We are going to remove the original graphic that is the black one and we will only leave the parts that represent our original graphic with the parts that intersect our red and blue functions:

Cool! What we have just represented can be written mathematically thanks to calculating the points of intersection of the original function $f (x)$ and once we write it we will already know how to perform our integral for the calculation of the area. Mathematically it is like this:

f(x) = \left\{ \begin{array}{l l l} x^{3} - x \quad & \text{ when } \quad & x \in [-1,0] \cup [1,\infty] \\ x - x^{3} & \text{ when } & x \in [-\infty,-1] \cup [0,1] \end{array}\right.

Taking advantage of the symmetry of the function, we can make an integral that goes from $0$ to $1$ and the result multiply it by $2$ , let’s see:

$\displaystyle A = \int_{0}^{1}(x - x^{3}) \ dx$

The integral of $x$ is $\frac{x^{2}}{2}$ and the integral of $x^{3}$ is $\frac{x^{4}}{4}$ :

$A = \left. \cfrac{x^{2}}{2} - \cfrac{x^{4}}{4} \right]_{0}^{1}$

We evaluate:

$A = \cfrac{1}{2} - \cfrac{1}{4} - 0 = \cfrac{1}{4}$

Now that obtained result we will multiply it by $2$ to obtain the total area:

$A = \cfrac{1}{4}(2) = \cfrac{1}{2} \ \text{u}^{2}$

So the total area of the function $|x^{3} - x|$ between the limits of $x=-1$ to $x=1$ equals $\frac{1}{2} \ \text{u}^{2}$

Thank you for being at this moment with us : )