Un sólido de revolución se genera al girar alrededor del eje y, la región acotada por la curva y = \sqrt[3]{x}, el eje x y la recta x = c donde c > 0. Calcular el valor de c para que el sólido tenga un volumen de 12 \pi u^{3}. La u^{3} significa unidades cúbicas.
Para hallar el volumen del sólido de revolución, utilizaremos el método de los cascarones cilíndricos.
Grafiquemos la función de y = \sqrt[3]{x} y coloquemos la recta x=c
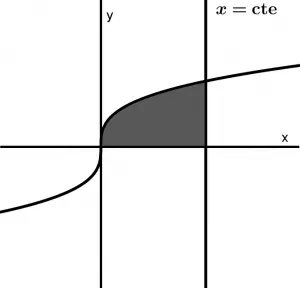Vamos a redactar la ecuación con la cual hallaremos el valor de c, lo que haremos es plantear una integral y la igualaremos al valor del volumen de 12 \pi u^{3} que nos dice el ejercicio, los límites de la integral tienen que ser desde cero hasta el valor de c:
\displaystyle V = \int_{0}^{c}2\pi x\sqrt[3]{x} = 12 \pi
Por propiedades de las integrales sacaremos las constantes de la integral y reduciremos las equis:
\displaystyle 2\pi \int_{0}^{c} x^{\frac{4}{3}} = 12 \pi
Cancelamos términos y efectuaremos la integral de x^{\frac{4}{3}} que, por regla de la cadena, es igual a \frac{3}{7}x^{\frac{7}{3}}:
\displaystyle \cancel{2}\cancel{\pi} \int_{0}^{2} x^{\frac{4}{3}} = \cancel{12} \cancel{\pi}
\left. \cfrac{3x^{\frac{7}{3}}}{7}\right]_{0}^{c} = 6
Evaluamos, multiplicaremos por 7 y dividiremos entre 3 toda la igualdad:
\cfrac{3c^{\frac{7}{3}}}{7} = 6
c^{\frac{7}{3}} = 14
Seguidamente elevaremos toda la igualdad al cubo para eliminar el denominador 3 de la potencia de \frac{7}{3}:
c^{7} = 14^{3} = 2744
Ahora sacaremos raíz a la 7 a toda la igualdad para obtener el valor de c:
c = \sqrt[7]{2744} \approx 3.098
Así que nuestro valor de c para que el volumen sea de 12\pi u^{3}, debe de tener un valor de \sqrt[7]{2744}.
Gracias por estar en este momento con nosotros : )
