El enunciado del ejercicio de optimización es el siguiente:
El buen Ramiro quiere construir una caja sin tapa cortando cuadrados en las esquinas de una hoja cuadrada de cartón de 60 cm por lado. Encuentra el tamaño del corte que se debe de realizar en las esquinas para que el volumen de la caja sea el máximo.
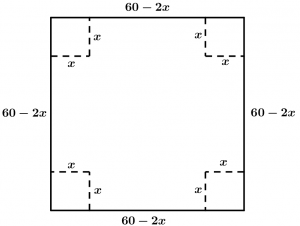
Bien, empezaremos con la representación gráfica del ejercicio, dibujaremos la hoja cuadrada de cartón con los respectivos cortes cuadrados de las esquinas que debemos hacerle.
Con el esquema de la caja, la parte más “complicada” (que es plantear la ecuación con la que se va a trabajar) se hace muy fácil. Para el cálculo del volumen se aplica la siguiente ecuación:
V=x(60-2x)^{2}
60-2x representa un lado de la caja que queremos armar y la x representa la altura de la caja. Como es una hoja de cartón cuadrada a la que se le quieren cortar cuadrados en las esquinas y el volumen es área de la base por la altura, el área de la base se calcula como lado por lado, o sea (60-2x)\cdot (60-2x)=(60-2x)^{2}, sólo falta multiplicar por la altura que es x. Y todo eso explica nuestra fórmula anterior del volumen.
Una vez que ya tengamos nuestra fórmula del volumen para nuestro ejercicio de optimización, vamos a resolver el binomio al cuadrado y luego lo vamos a multiplicar por la x:
V = x(3600 - 240x + 4x^{2})
= 3600x - 240x^{2} + 4x^{3}
Procedemos a realizar la derivada del volumen con respecto a x:
V'=3600 - 2(240)x+3(4)x^{2}
=3600-480x+12x^{2}
Ahora tenemos que igualar la ecuación a cero y bien podemos dividir todos los términos entre 12 para tener números más fáciles de manejar:
0 = x^{2} - 40x+ 300
Lo que se tiene que hacer es hallar los dos valores de x, puedes utilizar la famosa fórmula general o puedes buscar números en la ecuación al tanteo. Lo que nosotros hicimos fue buscar números en la ecuación al tanteo ya que resulta más rápido:
\begin{array}{c c c c c c c}
x^{2} & - & 40x & + & 300 & = & 0 \\\\
x & & & - & 10 & = & -10x \\
x & & & - & 30 & = & -30x \\
& & & & & = & -40x
\end{array}Lo que obtuvimos son dos valores, uno cuando x es igual a 10 y otro cuando x es igual a 30.
Utilizando un poquito de lógica, si utilizamos el valor de 30, y el valor del largo de la hoja cuadrada de cartón es igual a 60, no podremos armar ni una caja, sólo cortaríamos la hoja de cartón atravesando el centro, así que el valor de 30 lo descartamos.
Finalmente nuestra respuesta es igual a 10 cm. Así que el tamaño del corte que se debe de realizar para que el volumen sea el máximo es de 10 cm.
Gracias por estar en este momento con nosotros : )