Un pescador en bote de remos se encuentra a una distancia de 2 km mar adentro del punto más cercano de una playa recta y desea llegar a otro punto de la playa ubicado a 6 km del primero. Suponiendo que puede remar a una velocidad de 3 km/h y caminar a una velocidad de 5 km/h ¿Qué trayectoria debe seguir para llegar a su destino en el menor tiempo posible y cuál es el menor tiempo posible?
Veamos el siguiente esquema del pescador:
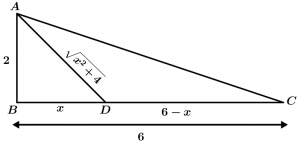El pescador se encuentra en A y tiene que remar a D para después caminar a C.
La fórmula que utilizaremos
Excelente, vas muy bien. Ahora lo que se tiene que hacer es saber qué fórmula hay que utilizar para calcular el menor tiempo posible. Conocemos muy bien la fórmula de velocidad que dice que velocidad (v) es igual a distancia (d) sobre tiempo (t):
v = \cfrac{d}{t}
Así que hay que despejar tiempo (t) para obtener la siguiente fórmula:
t = \cfrac{d}{v}
Las ecuaciones que se utilizarán para la función tiempo f(t)
Ahora vamos a plantear dos ecuaciones, una que vaya desde el punto A hasta el punto D y la otra que vaya desde el punto D hasta el punto C. Planteemos primero la del punto A hasta el punto D, tenemos la distancia (d) que es \sqrt{x^{2} + 4} y tenemos la velocidad (v) en la que el pescador rema que es 3km/h, recordando la fórmula de t = \frac{d}{v}, tendremos:
t = \cfrac{\sqrt{x^{2} + 4}}{3}
La segunda ecuación va desde el punto D hasta el punto C, tenemos la distancia (d) que es 6 - x y la velocidad (v) en la que el pescador camina en tierra que es 5 km/h, así que la ecuación es:
t = \cfrac{6 - x}{5}
Muy bien, tenemos las dos ecuaciones y fácilmente podemos expresarlas en una sola ecuación como una suma, así que nuestra función será la siguiente:
f(t) = \cfrac{\sqrt{x^{2} + 4}}{3} + \cfrac{6 - x}{5}
La parte más sencilla del ejercicio de optimización: derivar
Llegamos a la parte más sencilla de este ejercicio que es derivar, hay varias maneras de derivar f(t) y aquí vamos a aplicar la fórmula de la derivada de una fracción y además vamos a separar la fracción de \frac{6 - x}{5} en una resta por propiedades de las derivadas. Recordemos rápidamente la derivada de una división:
\left( \cfrac{a}{b} \right)' = \cfrac{ba' - ab'}{b^{2}}
Ahora sí, comencemos a derivar:
f'(t)=\left( \cfrac{\sqrt{x^{2} + 4}}{3} \right)' + \left( \cfrac{6}{5} \right)' - \left( \cfrac{x}{5} \right)'
La derivada de una constante es igual a cero, así que derivada de \frac{6}{5} es igual a cero y derivada de \frac{x}{5} es igual a \frac{1}{5}:
f'(t)=\cfrac{3(\sqrt{x^{2} + 4})' - \sqrt{x^{2} + 4}(3)'}{3^{2}} + 0 - \cfrac{1}{5}
Se aplicará la regla de la cadena a \left(\sqrt{x^{2} + 4}\right)' y la derivada de una constante es igual a cero, así que tendremos lo siguiente:
f'(t) = \cfrac{3\frac{1}{2} \left( x^{2} + 4\right)^{-\frac{1}{2}}(x^{2} + 4)' + (0)\sqrt{x^{2} + 4}}{9} - \cfrac{1}{5}
La derivada de (x^{2} + 4)' se puede dividir en una suma de derivadas como (x^{2})' + (4)' y el resultado es 2x, así que sustituiremos ese resultado en la ecuación:
f'(t)=\cfrac{3\frac{1}{2} \left( x^{2} + 4\right)^{-\frac{1}{2}}(2x)}{9} - \cfrac{1}{5}
E iremos cancelando términos:
f'(t) = \cfrac{\cancel{3}\frac{1}{2} \left( x^{2} + 4\right)^{-\frac{1}{2}}(2x)}{\cancel{9}} - \cfrac{1}{5}=
f'(t)= \cfrac{\frac{1}{\cancel{2}}\left( x^{2} + 4\right)^{-\frac{1}{2}}(\cancel{2}x) }{3} - \cfrac{1}{5}=
f'(t) = \cfrac{\left(x^{2} + 4 \right)^{-\frac{1}{2}}(x)}{3} - \cfrac{1}{5}
Con álgebra, el (x^{2} + 4)^{-\frac{1}{2}} pasa al denominador para eliminar el exponente negativo:
f'(t)=\cfrac{x}{3\left(x^{2} + 4\right)^{\frac{1}{2}}} - \cfrac{1}{5}=
f'(t)=\cfrac{x}{3\sqrt{x^{2} + 4}} - \cfrac{1}{5}
Igualemos la derivada a cero
Se tiene que igualar la derivada a cero para hallar los puntos críticos, los cuales nos servirán para saber en dónde la función f(t) es creciente y en dónde es decreciente:
\cfrac{x}{3\sqrt{x^{2} + 4}} - \cfrac{1}{5} = 0
Despejamos el -\frac{1}{5}:
\cfrac{x}{3\sqrt{x^{2} + 4}} = \cfrac{1}{5}
Pasamos multiplicando los denominadores:
5x = 3\sqrt{x^{2} + 4}
Elevamos al cuadrado:
(5x)^{2} = \left( 3\sqrt{x^{2} + 4}\right)^{2}=
25x^{2} = 9(x^{2} + 4)
Multiplicamos el 9 por el paréntesis:
25x^{2} = 9x^{2} + 36
Restamos el 9x^{2}:
25x^{2} - 9x^{2} = 36
16x^{2} = 36
Pasamos dividiendo el 16:
x^{2} = \cfrac{36}{16}
Sacamos raíz cuadrada a la igualdad:
\sqrt{x^{2}} = \pm\sqrt{\cfrac{36}{16}}
x = \pm\cfrac{\sqrt{36}}{\sqrt{16}}
x = \pm\cfrac{6}{4}
Simplificamos y finalmente tenemos nuestros puntos críticos:
x = \pm \cfrac{3}{2}
Veamos si tiene máximo o mínimo
Ahora lo que tenemos que hacer es establecer intervalos, tomar algún punto de prueba y evaluarlos en la función f'(t) para obtener las pendientes que nos dirán en qué momento la función cambia de decreciente a creciente:
\begin{array}{c | c | c | c}
\text{Intervalo} & \text{Valor Prueba} & \text{Signo de la Pendiente} & \text{Conclusión} \\
\hline
(-\infty,-3/2) & -2 & - & \text{Decreciente} \\
(-3/2,3/2) & 0 & - & \text{Decreciente} \\
(3/2,\infty) & 2 & + & \text{Creciente}
\end{array}¡Mira eso, hay un mínimo! Se dice que hay un mínimo porque va de decreciente y luego pasa a creciente, lo que quiere decir que el mínimo está cuando x vale 3/2, así que el valor que x necesita tener para que tengamos el mínimo es:
x = \cfrac{3}{2} = 1.5
Recordemos la gráfica que se propuso para el pescador:
Así que para que el pescador pueda llegar en el menor tiempo posible, tiene que remar de A a D una distancia de \sqrt{(1.5)^{2} + 4} = 2.5 \ km y además tiene que caminar de D hasta C una distancia de 6 - 1.5 = 4.5 \ km
¡Eso no es todo!
Recuerda que el ejercicio nos pide calcular el menor tiempo que se tardará el pescador en llegar a C, así que como ya tenemos las distancias óptimas que tiene que recorrer, sólo hay que utilizar reglas de 3 para calcular los tiempos, calculemos el tiempo que remará el señor pescador:
\begin{array}{c c c}
3 \ km & \rightarrow & 60 \ min \\
2.5 \ km & \rightarrow & t
\end{array}t = \cfrac{2.5 \ km \cdot 60 \ min}{3 \ km} = 50 \ min
Calculemos el tiempo que caminará el señor pescador:
\begin{array}{c c c}
5 \ km & \rightarrow & 60 \ min \\
4.5 \ km & \rightarrow & t
\end{array}t = \cfrac{4.5 \ km \cdot 60 \ min}{5 \ km} = 54 \ min
Ahora sumemos los tiempos:
50 \ min + 54 \ min = 104 \ min
Finalmente
El menor tiempo en el que el pescador puede llegar del punto A al punto C remando y caminando es de 104 minutos.
Gracias por estar en este momento con nosotros : )
