Se quiere construir una cisterna en forma de un prisma rectangular de base cuadrada que contenga una capacidad de 15 \ m^{3}. Si por las caras laterales y por la base se paga 10 dólares por m^{2} y por la parte superior se paga el doble por m^{2}, determina las dimensiones que debe de tener la cisterna para que el costo sea mínimo.
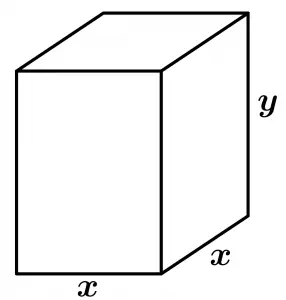
Para este problema de optimización de cálculo veremos a continuación una representación de la cisterna
Vamos a escribir la función que utilizaremos para el cálculo del costo mínimo. El costo es igual a la suma de algo que es lo que se planteará ahora. El costo de la base es igual al área de la base por el precio que será: 10x^{2}; más el costo de cada lado de la cisterna que es el área de cada lado multiplicado por 4 multiplicado por el precio: 4\cdot 10 xy = 40xy; más el costo de la tapa que tiene un área igual que la base pero el precio es el doble, en vez de escribir 10x^{2}, 20x^{2}. Con todo esto podemos escribir la siguiente función:
C(x) = 10x^{2} + 40xy + 20x^{2}
Reducimos términos:
C(x) = 30x^{2} + 40xy
Bien, pero no podemos derivar así porque sí, hace falta una ecuación más, la otra ecuación que hace falta es la del volumen:
V = 15 \ m^{3}
Pero el volumen igual se puede representar de la siguiente forma:
V = x^{2} \cdot y
Mira esta magia, vamos a igualar las ecuaciones del volumen que acabamos de plantear:
x^{2} \cdot y = 15 \ m^{3}
Y dejamos a solas a la y:
y =\cfrac{15}{x^{2}}
Con la ecuación recientemente obtenida, sustituiremos a la y en la función del costo:
C = 30x^{3} + 40x\left( \cfrac{15}{x^{2}}\right)
Multiplicamos:
C = 30x^{2} + \cfrac{600}{x}
Vamos a derivar la ecuación de optimización
C'(x) = 2\cdot 30 x + (600x^{-1})'
C'(x) = 60x +(-1)(600x^{-2})
C'(x) = 60x - (600x^{-2})
C'(x) = 60x - \cfrac{600}{x^{2}}
Ya que tenemos la primera derivada, vamos a igualar a cero y luego vamos a evaluar para obtener en donde es creciente y decreciente para saber si tiene mínimo:
0 = 60x - \cfrac{600}{x^{2}}=x\left( 60 - \cfrac{600}{x^{3}}\right)
Una x se hace cero, sólo falta calcular la otra:
60 = \cfrac{600}{x^{3}}
x^{3} = \cfrac{600}{60}=10
x = \sqrt[3]{10}\approx 2.15
Ahora hay que evaluar el valor prueba en la ecuación de la primera derivada para saber en dónde hay mínimo y en dónde hay máximo, veamos la siguiente tabla:
\begin{array}{c | c | c | c}
\text{Intervalo}& \text{Valor Prueba} & \text{Signo Resultado} & \text{Conclusión} \\
\hline
(-\infty, 0) & -1 & - & \text{Decreciente} \\
(0,\sqrt[3]{10}) & 1 & - & \text{Decreciente} \\
(\sqrt[3]{10}, \infty) & 3 & + &\text{Creciente} \\
\end{array}Lo que se puede observar, es que hay un mínimo cuando x = \sqrt[3]{10} porque va de decreciente a creciente.
Listo, eso es todo, una vez con nuestro mínimo ya hallado, hay que hallar el valor de y, agarramos la ecuación y = \frac{15}{x^{2}} y sustituimos x por \sqrt[3]{10}:
y = \cfrac{15}{\left( \sqrt[3]{10}\right)^{2}} \approx 3.23
Así que las dimensiones que debe de tener son de x = \sqrt[3]{10}\approx 2.15 \ m y y \approx 3.23 \ m.
Gracias por estar en este momento con nosotros : )