Comencemos primero con la fórmula de la longitud de arco y después veremos un ejercicio sencillo. Te recomendamos tengas una buena calculadora para que puedas comprobar tu resultado al final, una buena calculadora y económica es la Casio FX-991EX.
Fórmula de longitud de arco
\displaystyle L = \int_{a}^{b}\sqrt{1 + \left[ f'(x)\right]^{2}} \ dx
Ahora que ya tenemos la poderosa fórmula para calcular la longitud de arco, vamos con un ejemplo.
Ejemplo de longitud de arco
Calcular la longitud de arco de y=x^{2} desde x=0 hasta x=1.
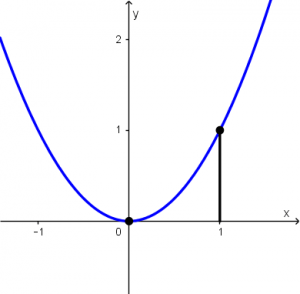La derivada de f(x)=x^{2} es f'(x) = 2x, así que sustituyamos en la fórmula de la longitud de arco la derivada y los límites.
\displaystyle L = \int_{0}^{1}\sqrt{1 + \left[ 2x \right]^{2}} \ dx
\displaystyle L = \int_{0}^{1}\sqrt{1 + 4x^{2}} \ dx
Para poder resolver este ejercicio utilizaremos trigonometría, vamos a ayudarnos del siguiente triángulo:
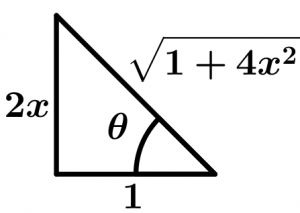Con el cual plantearemos las siguientes ecuaciones para poder dejar en términos trigonométricos la integral:
\tan \theta = 2x
\sec \theta = \sqrt{1 + 4x^{2}}
Derivamos \tan \theta para obtener:
\sec^{2}\theta \ d \theta = 2 \ dx
Ahora despejamos el 2 para dejar a la dx sola:
\cfrac{\sec^{2} \theta}{2} \ d \theta = dx
Una vez que ya tengamos las ecuaciones anteriores, sustituyamos en la integral de la longitud de arco de nuestro ejercicio:
\displaystyle L = \int_{0}^{1} \sqrt{1 + 4x^{2}} \ dx \Rightarrow
\displaystyle L = \int_{0}^{1} \sec \theta \ \cfrac{\sec^{2} \theta}{2} \ d\theta
Multiplicaremos los secantes para obtener un secante al cubo y por propiedades de las integrales podemos sacar el 2 del denominador
\displaystyle L = \cfrac{1}{2} \int_{0}^{1}\sec^{3} \theta \ d \theta
Consultando la integral de secante al cubo, obtendremos lo siguiente:
= \left. \cfrac{1}{4}\sec \theta \tan \theta + \cfrac{1}{4} \ln \left| \sec \theta + \tan \theta \right| \right]_{0}^{1}
Ahora, sustituyendo de vuelta a los valores de x, recuerda que \tan \theta = 2x y \sec \theta = \sqrt{1+ 4x^{2}}, obtendremos:
= \cfrac{1}{4} \left[ 2x \sqrt{1 + 4x^{2}} + \ln \left| \sqrt{1 + 4x^{2}} + 2x\right|\right]_{0}^{1}
Ahora sí, evaluando los límites obtendremos lo siguiente:
= \cfrac{1}{4} \left[\left( 2\sqrt{5} + \ln\left| 2 + \sqrt{5}\right|\right) - \left(0 \right) \right]
Finalmente obtenemos un resultado de:
L = \cfrac{2\sqrt{5} + \ln\left| 2 + \sqrt{5}\right|}{4}
Así que nuestra longitud de arco es:
L = \cfrac{2\sqrt{5} + \ln\left| 2 + \sqrt{5}\right|}{4}\approx 1.48 \ u
La u significa unidades.
Gracias por estar en este momento con nosotros : )
