Hallar la longitud de arco de x = 3y^{3/2} + 1 desde y=0 hasta y = 4.
Primero grafiquemos la función para tenerla más claramente:
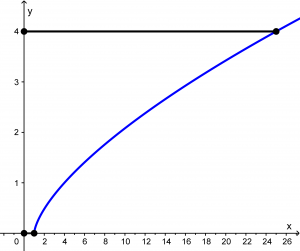 Ahora podemos proceder con la derivada de la función:
Ahora podemos proceder con la derivada de la función:
x = 3y^{3/2} + 1
x' = \cfrac{9}{2} y^{1/2}
Genial, con la derivada ya hecha, podemos sustituir en la fórmula de longitud de arco:
\displaystyle L = \int_{0}^{4} \sqrt{1 + \left[\cfrac{9y^{1/2}}{2} \right]^{2}} \ dy
Elevamos al cuadrado la fracción y sumamos:
\displaystyle = \int_{0}^{4} \sqrt{1 + \cfrac{81}{4} y}\ dy
\displaystyle = \int_{0}^{4} \sqrt{\cfrac{4 + 81y}{4}}\ dy
Sacaremos raíz cuadrada al denominador 4 y lo sacaremos de la integral:
\displaystyle =\int_{0}^{4} \cfrac{\sqrt{4 + 81y}}{2} dy= \cfrac{1}{2} \int_{0}^{4} \sqrt{4 + 81y} \ dy
Para resolver esa integral lo que haremos es sustituir 4 + 81y con la letra u y luego la derivaremos:
u = 4 + 81y
du = 81dy\quad \Rightarrow \quad \cfrac{du}{81} = dy
Ahora procedamos a sustituir en la integral:
\displaystyle =\cfrac{1}{2} \int_{0}^{4} \sqrt{u} \cfrac{du}{81}
\displaystyle =\cfrac{1}{162} \int_{0}^{4} \sqrt{u} \ du
Procedemos a realizar la integral, para que se haga más fácil tomaremos la raíz cuadrada como exponente a la un medio:
\displaystyle =\cfrac{1}{162} \int_{0}^{4} u^{1/2} \ du
= \left. \cfrac{1}{162} \cdot \cfrac{2u^{3/2}}{3}\right]_{0}^{4}
Efectuamos las multiplicaciones y divisiones correspondientes:
= \left. \cfrac{u^{3/2}}{243} \right]_{0}^{4}
Ahora hay que sustituir de vuelta la u, recuerda que u = 4 + 81y:
L = \left. \cfrac{\left(4 + 81y \right)^{3/2}}{243} \right]_{0}^{4}
Evaluamos:
L = \left[ \left( \cfrac{\left( 328\right)^{3/2}}{243} \right) - \left( \cfrac{8}{243} \right)\right]
=\cfrac{8\left(82 \right)^{3/2} - 8}{243}
En la fracción podemos factorizar el 8 y de igual forma podemos sacar el denominador:
\cfrac{8}{243} \left( 82^{3/2} - 1\right) \ \text{u}
La \text{u} significa unidades.
¡Así que finalmente ya tenemos nuestro resultado de la longitud de arco de este ejemplo!
L = \cfrac{8}{243} \left( 82^{3/2} - 1\right) \ \text{u}\approx 24.41
Gracias por estar en este momento con nosotros : )
