Calcular la longitud de arco de 24xy = x^{4}+48 desde x=2 hasta x=4.
Para resolver este ejercicio, vamos a dejar sola la y para poder proceder con al derivada, así que tenemos que pasar dividiendo el 24x para obtener:
y = \cfrac{x^{4} + 48}{24x}
Ahora, es recomendable graficar la función para tener más clara la longitud a calcular, así que la gráfica se verá de la siguiente forma:
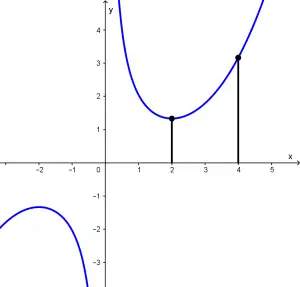Dividamos la fracción de una suma en una suma de fracciones y simplifiquemos:
y = \cfrac{x^{4}}{24x} + \cfrac{48}{24x}
y = \cfrac{x^{3}}{24} + \cfrac{2}{x}
Ahora procedamos con la derivada. La derivada de \frac{x^{3}}{24} es igual a \frac{x^{2}}{8} y la derivada de \frac{2}{x} es igual a -\frac{2}{x^{2}}:
y' = \cfrac{x^{2}}{8} - \cfrac{2}{x^{2}} = \cfrac{x^{4} - 16}{8x^{2}}
Ahora podemos utilizar la fórmula de la longitud de arco para hallar dicha longitud, recuerda que los límites son de 2 a 4:
\displaystyle L = \int_{2}^{4}\sqrt{1 + \left[ \cfrac{x^{4} - 16}{8x^{2}} \right]^{2}} \ dx
Elevando al cuadrado, obtendremos:
\displaystyle =\int_{2}^{4}\sqrt{1 + \cfrac{x^{8} - 32x^{4} + 256}{64x^{4}}}
Realicemos la suma de fracciones (porque el 1 tiene denominador 1) y simplifiquemos:
\displaystyle =\int_{2}^{4}\sqrt{\cfrac{64x^{4} + x^{8} - 32x^{4} + 256}{64x^{4}}}
\displaystyle =\int_{2}^{4}\sqrt{\cfrac{x^{8} + 32x^{4} + 256}{64x^{4}}}
Factorizamos:
\displaystyle =\int_{2}^{4}\sqrt{\cfrac{\left( x^{4} + 16\right)^{2}}{64x^{4}}}
Y sacaremos raíz cuadrada:
\displaystyle =\int_{2}^{4}\cfrac{x^{4} + 16}{8x^{2}}
Ahora, por propiedades de las integrales, sacaremos el denominador 8 y luego separaremos la integral de una suma en una suma de integrales:
=\cfrac{1}{8}\int_{2}^{4} \cfrac{x^{4} + 16}{x^{2}}
\displaystyle =\cfrac{1}{8} \int_{2}^{4} x^{2} \ dx + 2 \int_{2}^{4} \cfrac{dx}{x^{2}}
Integremos, la integral de x^{2} es igual a \frac{x^{3}}{3} y la integral de \frac{1}{x^{2}} es igual a -\frac{1}{x}:
=\left. \cfrac{x^{3}}{24} - \cfrac{2}{x} \right]_{2}^{4}
Evaluando:
=\left( \cfrac{8}{3} - \cfrac{1}{2} \right) - \left(\cfrac{1}{3} - 1 \right)
Resolviendo las operaciones, obtendremos:
= \cfrac{17}{6} \ \text{u}
La \text{u} significa unidades.
¡Así obtenemos nuestro resultado final de longitud de arco!
L = \cfrac{17}{6} \ \text{u} \approx 2.83 \ \text{u}
Gracias por estar en este momento con nosotros : )