Fórmula para hallar la longitud de arco
\displaystyle S = \int_{\alpha}^{\beta}\sqrt{\left( \cfrac{d\rho}{d\theta}\right)^{2} + \rho^{2}} \ d \theta
Ejemplo. Calculemos la longitud de arco de un cardioide
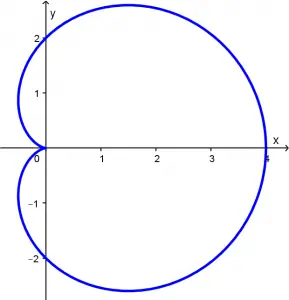
El cardioide al cual vamos a hallar su longitud de arco es \rho = 2(1 + \cos \theta), gráficamente se ve así:
\rho = 2(1 + \cos \theta)
Como dice en la fórmula, necesitamos calcular la derivada de \rho. Para hacerlo, vamos a multiplicar el 2 con el paréntesis:
\rho = 2 + 2 \cos \theta
Y ahora sí procedemos a derivar, derivada de una constante es igual a cero y derivada de coseno es igual a menos seno:
\rho ' = 0 - 2\sin \theta
\rho ' = -2 \sin \theta
Lo que hay que hacer es sustituir en la integral los valores de la derivada y del cuadrado de \rho:
\displaystyle S = \int_{\alpha}^{\beta}\sqrt{(-2\sin \theta)^{2} + (2(1 + \cos \theta))^{2}} \ d\theta
Una vez que ya tengamos nuestra integral para resolver, podemos comprobar la respuesta para saber que todo el procedimiento que hicimos es correcto. Una calculadora que recomendamos es la Casio FX-991EX, sólo que recuerda que cuando la utilices tienes que ponerla en radianes y el límite va de cero a \pi en caso de que multipliques por 2 el resultado, y en caso de que no lo multipliques por dos pones los límites de cero a 2\pi.
¿Y nuestros límites de los ángulos en radianes \alpha y \beta cuáles son?
Hay dos opciones de colocar los límites en la integral. La primera opción es colocar los límites de cero a \pi, que el resultado sólo nos dará la mitad del valor de la longitud completa, lo que quiere decir que hay que multiplicar por 2 el resultado. La segunda opción es colocar los límites de cero a 2\pi, que representa que vas a dar de una vez toda la vuelta al cardioide. Con las dos opciones se llega al mismo resultado, continuemos:
Colocaremos un 2 a la integral porque sólo vamos a integrar de cero a \pi y elevamos al cuadrado para obtener:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{4\sin^{2}\theta + 4(1 + 2 \cos \theta + \cos^{2} \theta)} \ d\theta
Multipliquemos el paréntesis donde está el 4:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{4\sin^{2} \theta + 4 + 8 \cos \theta + 4 \cos^{2} \theta} \ d \theta
Vamos a ordenar el término 4\sin^{2} \theta y el término 4\cos^{2} \theta y factorizaremos el 4:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{4(\sin^{2}\theta + \cos^{2} \theta) + 4 + 8 \cos \theta} \ d \theta
Recordemos una identidad trigonométrica muy poderosa:
\sin^{2}\theta + \cos^{2}\theta = 1
Con la identidad trigonométrica, reduzcamos términos:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{4 + 4 + 8\cos \theta} \ d \theta
Sumemos los 4:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{8 + 8\cos \theta} \ d \theta
Vamos a factorizar el 8:
\displaystyle S = 2\int_{0}^{\pi}\sqrt{8(1 + \cos \theta)} \ d \theta
Y ese 8 lo podemos representar como 2^{2}\cdot 2:
\displaystyle S = 2 \int_{0}^{\pi}\sqrt{2^{2}\cdot 2(1 + \cos \theta)} \ d \theta
Ese 2^{2}\cdot 2 lo podemos sacar de la raíz cuadrada para después, por propiedades de integrales, sacarlo de la integral:
\displaystyle S = 2 \int_{0}^{\pi} \left(2\sqrt{2} \right) \sqrt{1 + \cos \theta} \ d \theta
\displaystyle S = 2\left( 2\sqrt{2}\right)\int_{0}^{\pi}\sqrt{1 + \cos \theta} \ d\theta
Multipliquemos términos:
\displaystyle S = 4\sqrt{2}\int_{0}^{\pi}\sqrt{1 + \cos \theta} \ d \theta
Bueno, ¿y eso cómo se integra?
Tranquilo, eso se integra fácilmente utilizando la siguiente identidad trigonométrica:
\cos^{2}\left(\cfrac{\theta}{2}\right) = \cfrac{1+\cos \theta}{2}
Esa identidad trigonométrica le aplicaremos raíz cuadrada para obtener:
\cos \left( \cfrac{\theta}{2}\right) = \cfrac{\sqrt{1 + \cos \theta}}{\sqrt{2}}
Ahora a la integral a la que llegamos le vamos a multiplicar y a dividir una \sqrt{2} para que sea igual a la identidad trigonométrica:
\displaystyle S = 4\sqrt{2} \int_{0}^{\pi} \sqrt{2}\cfrac{\sqrt{1 + \cos \theta}}{\sqrt{2}} \ d \theta
Por propiedades de integrales, sacaremos el \sqrt{2} de la integral que se encuentra como numerador:
\displaystyle S = 4 \sqrt{2}\cdot\sqrt{2}\int_{0}^{\pi}\cfrac{\sqrt{1 + \cos \theta}}{\sqrt{2}} \ d \theta
¡Ahora nuestra integral se parece a lo que hicimos en la identidad trigonométrica! Sólo sustituyamos lo que está en la integral por \cos \left( \frac{\theta}{2}\right) y multipliquemos de una vez a las dos raíces cuadradas de dos y al cuatro:
\displaystyle S = 8\int_{0}^{\pi}\cos \left( \cfrac{\theta}{2} \right) \ d \theta
Para resolver esa integral, llamaremos u a \frac{\theta}{2}, derivaremos y despejaremos:
u = \cfrac{\theta}{2}
du = \cfrac{d\theta}{2}
2 \ du = d \theta
Sustituyamos esos términos en la integral:
\displaystyle S = 8 \int_{0}^{\pi} \cos (u ) (2 \ du)
Apliquemos propiedades de integrales para sacar el dos y multipliquémoslo con el 8:
S = 16 \int_{0}^{\pi}\cos(u) \ du
Recordemos que la integral de coseno es igual a seno, así que integremos:
S = 16 \left. \sin(u)\right|_{0}^{\pi}
Regresemos el \frac{\theta}{2}:
S = 16 \left. \sin\left( \cfrac{\theta}{2} \right) \right|_{0}^{\pi}
Utilizando una calculadora en radianes, evaluemos el seno:
S = 16 \left( 1 -0\right)
Y finalmente nuestro resultado de la longitud de arco del cardioide es:
S = 16 \ \text{u}
La u del resultado final significa “unidades”, o sea la longitud es de 16 unidades.
Mira el siguiente video del post
Gracias por estar en este momento con nosotros : )