El siguiente ejemplo de la integral definida es:
Hallar la integral de f(x) = (x^{3} - x) dentro de los límites de -1 a 2:
\displaystyle \int_{-1}^{2}(x^{3} - x) dx
En este ejemplo de integral definida vamos a bosquejar la función sólo para tenerla visualmente, para poder hacer eso vamos a factorizar y a igualar a cero la función y hallaremos los puntos de intersección:
0 = (x^{3} - x)
0 = x(x^{2} - 1)
Como se puede observar, tenemos un punto de intersección en cero y los otros dos puntos de intersección los tenemos en uno y en menos uno:
x = 0 \qquad x = 1 \qquad x = -1
Ahora que tenemos los puntos de intersección de la función de la integral definida, la bosquejaremos y sombrearemos el área a hallar dentro de los límites que nos dice la integral:
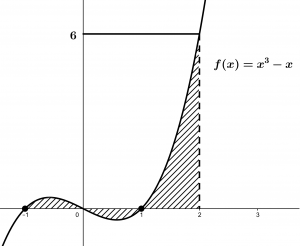Genial, ahora que ya tenemos bosquejada la función, procedamos con la integral, podemos consultar aquí para recurrir a las fórmulas de las integrales:
\displaystyle \int_{-1}^{2}(x^{3} - x) \ dx = \cfrac{x^{4}}{4} - \cfrac{x^{2}}{2} = \cfrac{x^{2} - 2x^{2}}{4}
Ahora continuaremos con la evaluación de los límites:
= \left. \cfrac{x^{4} - 2x^{2}}{4} \right]_{-1}^{2}
\begin{array}{c c c}
\text{Evaluamos en }2 & \qquad & \text{Evalamos en} -1 \\
\cfrac{(2)^{4} - 2(2)^{2}}{4} = 2& & \cfrac{(-1)^{4} - 2(-1)^{2}}{4} = -\cfrac{1}{4}
\end{array}Resolvemos unas operaciones simples:
2 -\left(- \cfrac{1}{4} \right)= 2 + \cfrac{1}{4}
Y así obtenemos que el área sombreada es igual a:
\cfrac{9}{4}u^{2}
Comprobemos la integral definida con límite de sumatoria de Riemann
Para poder comprobar una integral definida con una sumatoria de Riemann, lo que se tiene que recordar son las fórmulas siguientes:
\displaystyle A = \underset{n \to \infty} \lim \; \sum_{i = 1}^{n} f(c_{i})\Delta x
\Delta x = \cfrac{b - a}{n}
c_{i} = x_{i} = a + i\Delta x
El valor de a es el límite inferior de la integral y b es el valor del límite superior de la misma integral. Primero hallemos el valor de \Delta x:
\Delta x = \cfrac{2 - (-1)}{n} = \cfrac{3}{n}
Ya que tenemos \Delta x, vamos a hallar c_{i}:
c_{i} = -1 + i\Delta x
Ese valor de c_{i} lo sustituiremos en nuestra función f(x), así obtendremos lo siguiente:
f(c_{i}) = (-1 + i \Delta x)^{3} - ( -1 + i \Delta x)
Elevando al cubo obtendremos la siguiente expresión:
f(c_{i}) = \cancel{-1} + 3i\Delta x - 3i^{2}\Delta x^{2} + i^{3} \Delta x^{3} \cancel{+1} - i\Delta x
Así, el valor de f(c_{i}) es:
=i^{3} \Delta x^{3} - 3i^{2} \Delta x^{2} + 2i \Delta x
Vamos con la sustitución
Sustituyamos la f(c_{i}) y la \Delta x que salen en la función de área del límite de la sumatoria de Riemann:
\displaystyle A = \underset{n \to \infty} \lim \; \sum_{i = 1}^{n} f(c_{i})\Delta x
\displaystyle =\underset{n\to\infty}\lim\; \sum_{i=1}^{n}(i^{3} \Delta x^{3} - 3i^{2} \Delta x^{2} + 2i\Delta x)\cfrac{3}{n}
Aplicando propiedades de la sumatoria, podemos escribir lo siguiente:
\displaystyle \underset{n \to \infty} \lim \; \cfrac{3}{n}\left[ \Delta x^{3} \sum_{i=1}^{n} i^{3} - 3\Delta x^{2} \sum_{i=1}^{n} i^{2} + 2\Delta x\sum_{i = 1}^{n}i \right]
Sólo falta efectuar esas sumatorias, para hacer más rápido tantas operaciones, en propiedades de la sumatoria encontrarás las sumatorias ya realizadas, sólo sustituyamos:
\underset{n\to \infty}\lim\; \cfrac{3}{n} \left[ \Delta x^{3} \cfrac{(n^{2}(n+1)^{2})}{4} - 3\Delta x^{2}\cfrac{(n(n+1)(2n+1))}{6} + 2\Delta x \cfrac{n(n+1)}{2}\right]
Ahora esos \Delta x los podemos sustituir con los \frac{3}{n} para obtener lo siguiente:
=\underset{n\to\infty}\lim\; \cfrac{3}{n} \left[ \left( \cfrac{27}{n^{3}}\right) \cfrac{(n^{4} + 2n^{3} + n^{2})}{4} - 3\left( \cfrac{9}{n^{2}}\right) \cfrac{(2n^{3} + 3n^{2} + n)}{6} +\cancel{2} \left( \cfrac{3}{\cancel{n}} \cfrac{(n^{\cancel{2}} + \cancel{n})}{\cancel{2}}\right) \right]
Efectuando las operaciones dentro de los corchetes, obtendremos lo siguiente:
=\underset{n\to\infty}\lim\; \cfrac{3}{n} \left[ \cfrac{27n}{4} + \cancel{\cfrac{27}{2}} + \cfrac{27}{4n} - 9n - \cancel{\cfrac{27}{2}} - \cfrac{9}{2n} + 3n + 3 \right]
Ahora aplicaremos límites:
=\underset{n\to\infty}\lim\; \cfrac{81}{4} + \cancel{\cfrac{81}{4n^{2}}} - 27 - \cancel{\cfrac{3}{2n^{2}}} + 9 + \cancel{\cfrac{9}{n}}
= \cfrac{81}{4} - 27 + 9
Simplificando obtendremos como resultado:
A = \cfrac{9}{4}u^{2}
¡Comprobando con la integral y con el límite de la sumatoria de Riemann, afirmamos que nuestro resultado de \frac{9}{4} es correcto!
Gracias por estar en este momento con nosotros : )
