Las integrales por sustitución trigonométrica parecen ser difíciles pero con la siguiente explicación creemos que podrían quedar bastante claras como para poder dominar este estilo de integrales.
Se presentan 3 casos del método de integración por sustitución trigonométrica, veremos la explicación de cada caso y seguidamente de cada explicación mostraremos un ejemplo. ¡Comencemos!
Primer caso de integrales por sustitución trigonométrica
Explicación
Cuando en una integral tengamos la forma \sqrt{a^{2} - x^{2}} se utilizará la sustitución de x = a \ \sin \theta. Recordando que a siempre va a tener un valor mayor que cero. Así que:
\sqrt{a^{2} - x^{2}} \quad \Rightarrow \quad x = a \ \sin \theta
Ejemplo
Resolver la integral siguiente:
\displaystyle \int \cfrac{\sqrt{9 - x^{2}}}{x^{2}} \ dx
En la integral presentada el valor de a no es 9, el valor de a es 3. Hay que tener cuidado con esto ya que las primeras veces uno llega a confundirse con eso. Genial, una vez que ya tengamos definida que a es 3, vamos a sustituir el valor de x:
x = 3 \sin \theta
Una vez que ya tenemos la sustitución, tenemos que hallar todos los demás elementos de la integral con nuestra sustitución, vamos a elevar x al cuadrado y vamos a derivar x. La derivada es:
dx = 3 \cos \theta \ d\theta
Y x^{2} es:
x^{2} = 9 \sin^{2}\theta
Bien, para no tener que escribir todos los elementos de la integral tantas veces, tomaremos \sqrt{9-x^{2}}, sustituiremos x^{2} y lo simplificaremos lo más que podamos, veamos:
\sqrt{9 - x^{2}} = \sqrt{9 - 9 \sin^{2} \theta}
Procederemos a factorizar el 9:
=\sqrt{9\left( 1 - \sin^{2} \theta\right)}
¡Mira! Esa identidad trigonométrica la conocemos muy bien, sabemos que \cos^{2}\theta = 1 - \sin^{2} \theta, así que procedemos a sustituir en la raíz:
=\sqrt{9\cos^{2} \theta}
Sacando raíz cuadrada al 9 da como resultado 3 y raíz cuadrada de \cos^{2}\theta da como resultado \cos \theta:
= 3 \cos \theta
Ahora retomamos nuestra integral y sustituimos, recordando que \sqrt{9-x^{2}} = 3\cos \theta, x^{2} = 9 \sin^{2} \theta y dx = 3 \cos \theta \ d \theta:
\displaystyle \int \cfrac{\sqrt{9 - x^{2}}}{x^{2}} \ dx =\int \cfrac{3 \cos \theta}{9 \sin^{2} \theta}3 \cos \theta d \theta
Cancelaremos el 9 del denominador con los 3 que hay en el numerador y multiplicaremos los \cos \theta del numerador:
\displaystyle = \int \cfrac{\cos^{2} \theta}{\sin ^{2} \theta} \ d \theta
Algo muy importante que hay que recordar es que \cfrac{\cos \theta}{\sin \theta} = \cot \theta, así que se tendrá:
\displaystyle = \int \cot^{2} \theta \ d \theta
En este momento se aplicará una identidad trigonométrica que dice que \cot^{2} \theta = \csc^{2} \theta - 1:
\displaystyle = \int \left( \csc^{2} \theta - 1 \right) \ d \theta
La integral ya está casi resuelta, aplicaremos propiedades de las integrales para que esa resta de la integral se convierta en una resta de integrales:
\displaystyle = \int \csc^{2} \theta \ d \theta - \int d \theta
La integral de \csc^{2} \theta es igual a - \cot \theta y la integral de d \theta es igual a \theta, no olviden el + \text{ C}:
= -\cot \theta - \theta + \text{C}
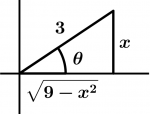
Ya casi terminamos, utilizando la sustitución trigonométrica de x = 3 \sin \theta, despejando el 3 obtendremos \cfrac{x}{3} = \sin \theta y recordemos que \sin \theta = \cfrac{\text{cateto opuesto}}{\text{hipotenusa}}, entonces nuestro cateto opuesto es x y nuestra hipotenusa es 3, el cateto adyacente es la raíz del cuadrado de la hipotenusa menos el cuadrado del cateto opuesto. Dibujemos el siguiente triángulo para ubicar mejor todo lo mencionado en el párrafo:
Como sabemos que x =3 \sin \theta, hay que despejar para dejar sola \theta, dando como resultado:
\theta = \sin^{-1} \cfrac{x}{3}
Y \cot \theta = \cfrac{\text{cateto adyacente}}{\text{cateto opuesto}}, entonces:
\cot \theta = \cfrac{\sqrt{9 - x^{2}}}{x}
Sustituimos estas (valga la redundancia) sustituciones en nuestro resultado para así finalmente obtener:
- \cfrac{\sqrt{9 - x^{2}}}{x^{2}} - \sin^{-1} \cfrac{x}{3} + \text{C}
Segundo caso de integrales por sustitución trigonométrica
Explicación
Cuando en una integral tengamos la forma \sqrt{a^{2} + x^{2}} se utilizará la sustitución de x = a \ \tan \theta. Recordando que a siempre va a tener un valor mayor que cero. Así que:
\sqrt{a^{2} + x^{2}} \quad \Rightarrow \quad x = a \ \tan \theta
Ejemplo
Resolver la siguiente integral:
\displaystyle \int \sqrt{x^{2} + 5} \ dx
El valor de a^{2} es igual a 5, así que el valor de a es \sqrt{5}, con este dato podemos ya plantear la sustitución trigonométrica:
x = \sqrt{5} \tan \theta
Ahora lo que se tiene que hacer es derivar x y elevar x al cuadrado. Derivemos primero, derivada de \tan \theta es igual a \sec^{2} \theta \ d \theta:
dx = \sqrt{5} \sec^{2} \theta \ d\theta
Y elevemos al cuadrado a x:
x^{2} = 5 \tan^{2} \theta
Bien, tomaremos la raíz cuadrada de la integral para no andar escribiendo todos los elementos de la integral a cada rato, pero puede hacerlo como guste. Continuemos, hagamos la sustitución:
\sqrt{x^{2} + 5} = \sqrt{5\tan^{2} \theta + 5}
Factorizaremos el 5:
=\sqrt{5\left(\tan^{2} \theta + 1 \right)}
Aplicando identidades trigonométricas, podemos sustituir el \tan^{2}\theta + 1 por \sec^{2} \theta:
=\sqrt{5\sec^{2} \theta}
Y podemos aplicar raíz cuadrada para que \sec^{2} \theta sea \sec \theta:
= \sqrt{5} \sec \theta
Ya que tenemos la sustitución realizada, ahora sí vayamos a la integral y escribamos lo que acabamos de obtener y sustituyamos dx = \sqrt{5}\sec^{2} \theta \ d \theta y \sqrt{x^{2} + 5} = \sqrt{5} \sec \theta:
\displaystyle \int \sqrt{x^{2} + 5} \ dx= \int\sqrt{5} \sec \theta \cdot \sqrt{5} \sec^{2} \theta \ d\theta
Efectuaremos la multiplicación de las raíces de 5 para obtener el valor de 5 y multiplicaremos las secantes para obtener secante al cubo, además por propiedades de las integrales sacaremos de una vez de la integral el 5:
\displaystyle = 5 \int \sec^{3} \theta \ d\theta
Utilizando un formulario se puede observar que la integral de secante al cubo es la siguiente:
\cfrac{1}{2} \sec \theta \tan \theta + \cfrac{1}{2} \ln \left|\sec \theta + \tan \theta \right| + \text{C}
Así que recordando que la integral estaba multiplicada por 5, quedará de la siguiente manera:
\cfrac{5}{2} \sec \theta \tan \theta + \cfrac{5}{2} \ln \left|\sec \theta + \tan \theta \right| + \text{C}
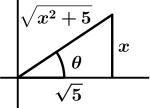
Ahora hay que regresar la sustitución para dejar con términos de x el resultado, necesitamos el triángulo que tiene los valores de la sustitución trigonométrica, recordando que x = \sqrt{5} \tan \theta tenemos el siguiente triángulo:
El triángulo se construye ya que como \tan \theta = \cfrac{\text{cateto opuesto}}{\text{cateto adyacente}}, entonces \tan \theta = \cfrac{x}{\sqrt{5}}, eso quiere decir que x es el valor del cateto opuesto y \sqrt{5} es el valor del cateto adyacente y el valor de la hipotenusa se calcula como la raíz de la suma de los cuadrados de los catetos o más resumido, con el Teorema de Pitágoras: c^{2} = a^{2} + b^{2}.
Ya que tenemos el triángulo, podemos pasar a sustituir:
\sec\theta = \cfrac{\text{hipotenusa}}{\text{cateto adyacente}}
\sec \theta = \cfrac{\sqrt{x^{2} + 5}}{\sqrt{5}}
Ahora vamos con tangente de theta:
\tan \theta = \cfrac{\text{cateto opuesto}}{\text{cateto adyacente}}
\tan \theta = \cfrac{x}{\sqrt{5}}
Genial, ya tenemos todos los cálculos realizados, ahora podemos pasar a sustituir en el resultado:
=\cfrac{5}{2} \left( \cfrac{\sqrt{x^{2} + 5}}{\sqrt{5}} \right) \left( \cfrac{x}{\sqrt{5}} \right) + \cfrac{5}{2}\ln \left|\cfrac{\sqrt{x^{2} + 5}}{\sqrt{5}} + \cfrac{x}{\sqrt{5}} \right| + \text{C}
Reduzcamos términos:
\cfrac{x\sqrt{x^{2} + 5}}{2} + \cfrac{5}{2} \ln \left|\cfrac{x + \sqrt{x^{2} + 5}}{\sqrt{5}} \right| + \text{C}
El logaritmo de la división se puede separar como una resta de logaritmos:
\cfrac{x\sqrt{x^{2} + 5}}{2} + \cfrac{5}{2} \ln \left| x + \sqrt{x^{2} + 5} \right| - \cfrac{5}{2} \ln \sqrt{5} + \text{C}
Aquí se puede hacer un “truco” para reducir términos, como el término de \frac{5}{2} \ln \sqrt{5} es una constante, se puede sumar a \text{C} ya que \frac{5}{2} \ln \sqrt{5} es una constante igual que \text{C}, observa cómo quedará nuestro resultado final de la integral:
= \cfrac{x\sqrt{x^{2} + 5}}{2} + \cfrac{5}{2} \ln \left|x + \sqrt{x^{2} + 5} \right| + \text{C}
Tercer caso de integrales por sustitución trigonométrica
Explicación
Cuando en una integral tengamos la forma \sqrt{x^{2} - a^{2}} se utilizará la sustitución de x = a \ \sec \theta. Recordando que a siempre va a tener un valor mayor que cero. Así que:
\sqrt{x^{2} - a^{2}} \quad \Rightarrow \quad x = a \ \sec \theta
Ejemplo
Resolver la integral siguiente:
\displaystyle \int \cfrac{dx}{x^{3}\sqrt{x^{2} - 9 }}
Antes de continuar quiero hacer una aclaración, observa que esta vez la raíz está en el denominador y multiplicado por una equis cúbica, quiero aclarar que no importa si la raíz está en el numerador o en el denominador, mientras se tenga la forma de la raíz para realizar la sustitución se puede hacer la sustitución, no hay una regla que diga que se necesita que la raíz esté en el denominador o en el numerador para hacer tal cosa. Mientras tenga la forma de la raíz de cualquier caso de sustitución trigonométrica se puede aplicar el caso que se requiera. Continuemos.
El valor de a^{2} es igual a 9, así que el valor de a es 3, con este dato podemos ya plantear la sustitución trigonométrica:
x = 3\sec \theta
Hay que derivar x, elevar al cuadrado y al cubo x, derivemos primero:
dx = 3 \sec \theta \tan \theta \ d \theta
El cuadrado de x es:
x^{2} = 9\sec^{2} \theta
Y el cubo de x es:
x^{3} = 27 \sec^{3} \theta
Tomaremos la raíz cuadrada para reducirla lo más posible, esto sólo se hace para no tener que andar escribiendo los demás elementos de la integral a cada rato, continuemos:
\sqrt{x^{2} - 9} = \sqrt{9\sec^{2} \theta - 9}
Vamos a factorizar el 9:
=\sqrt{9\left( \sec^{2} \theta - 1\right)}
Ahora lo que se puede apreciar es que tenemos una identidad trigonométrica, la que nos dice que \tan^{2}\theta = \sec^{2} \theta - 1, sustituyamos:
=\sqrt{9 \tan^{2} \theta}
Sacamos raíz cuadrada y listo, raíz cuadrada de 9 es 3 y raíz cuadrada de \tan^{2}\theta es \tan \theta:
= 3 \tan \theta
Genial, con esta sustitución vamos a reemplazar todas las x y simplificaremos, dx = 3\sec\theta \tan \theta \ d \theta, x^{3} = 27\sec^{3} \theta y \sqrt{x^{2} - 9} = 3\tan \theta:
\displaystyle \int\cfrac{dx}{x^{3}\sqrt{x^{2} - 9}} = \int \cfrac{3 \sec \theta \tan \theta \ d \theta}{27\sec^{3}\theta \left( 3\tan \theta\right)}
Vamos a simplificar, el 3 del numerador se cancela con el 3 del denominador, el secante al cubo pasa a ser secante al cuadrado y el secante del numerador se cancela, el tangente del numerador se cancela con el tangente del denominador y por propiedades de las integrales sacaremos al \frac{1}{27} de la integral, veamos:
\displaystyle = \cfrac{1}{27} \int \cfrac{d\theta}{\sec^{2} \theta}
Conociendo las funciones trigonométricas, \frac{1}{\sec^{2}\theta} = \cos^{2} \theta, así que nuestra integral quedará de la siguiente manera:
\displaystyle = \cfrac{1}{27} \int \cos^{2} \theta \ d \theta
En este momento hay que aplicar identidades trigonométricas para poder resolver la integral, observa a qué es igual el \cos^{2}\theta gracias a las identidades trigonométricas:
\cos^{2} \theta = \cfrac{1}{2} + \cfrac{1}{2} \cos 2\theta
Lo sustituimos en la integral:
\displaystyle = \cfrac{1}{27} \int \left( \cfrac{1}{2} + \cfrac{1}{2} \cos 2\theta\right) \ d \theta
Por propiedades de las integrales separaremos esa suma de la integral en una suma de integrales y de una vez multiplicaremos al 2 con el 27:
\displaystyle =\cfrac{1}{54}\int d \theta + \cfrac{1}{54} \int \cos 2 \theta \ d \theta
La integral de d\theta fácilmente es \theta:
\displaystyle =\cfrac{1}{54}\theta + \cfrac{1}{54} \int \cos 2\theta \ d \theta
Para resolver la integral que falta tenemos que hacer un cambio de variable, llamaremos u a 2\theta, sólo falta derivar u:
u = 2\theta
du = 2 d \theta
Pasamos dividiendo el 2:
\cfrac{du}{2} = d \theta
Y ahora sustituimos las variables en la integral. (Por el momento no escribiremos el resultado obtenido de \frac{1}{54}\theta, lo reescribiremos más adelante):
\displaystyle = \cfrac{1}{54} \int \cos u \ \cfrac{du}{2}
Por las propiedades de las integrales sacaremos el 2 para que multiplique a 54 y de una vez aplicamos la integral de coseno que es igual a seno:
=\cfrac{1}{108} \sin u
Sustituimos de vuelta el 2\theta:
=\cfrac{1}{108} \sin 2\theta
Reescribimos el otro resultado que omitimos y recuerden poner el +\text{C}:
=\cfrac{1}{54} \theta + \cfrac{1}{108}\sin 2\theta + \text{C}
Apliquemos otra identidad trigonométrica la cual dice que \sin 2\theta = 2\sin \theta \cos \theta, sustituyamos:
\cfrac{1}{54} \theta + \cfrac{1}{108}\left( 2\sin \theta \cos \theta\right)
Simplifiquemos:
\cfrac{1}{54} \theta + \cfrac{1}{54}\sin \theta \cos \theta + \text{C}
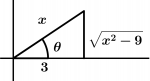
Y ahora, para dejar el resultado en términos de x, necesitamos el triángulo que nos lo dirá todo, recordando que x = 3 \sec \theta, \sec \theta = \cfrac{\text{hipotenusa}}{\text{cateto adyacente}} así que la hipotenusa será x y el cateto adyacente será 3, el cateto opuesto de \theta será la raíz del cuadrado de la hipotenusa menos el cuadrado del cateto adyacente, observemos el triángulo:
Como ya tenemos que x = 3\sec \theta, se tiene que despejar \theta, así que pasamos dividiendo el 3 a x y se obtendrá \frac{x}{3} = \sec \theta, aplicando secante inversa a la igualdad obtendremos el valor de \theta:
\theta = \sec^{-1}\cfrac{x}{3}
Recordemos que \sin \theta = \cfrac{\text{cateto opuesto}}{\text{hipotenusa}}, observando el triángulo:
\sin \theta = \cfrac{\sqrt{x^{2} - 9}}{x}
Recordando que \cos \theta = \cfrac{\text{cateto adyacente}}{\text{hipotenusa}}, observando el triángulo obtendremos que:
\cos \theta = \cfrac{3}{x}
Así que, sustituyendo todos los valores, tenemos nuestro resultado final:
=\cfrac{1}{54} \sec^{-1}\cfrac{x}{3} + \cfrac{1}{18} \left( \cfrac{\sqrt{x^{2} - 9}}{x^{2}} \right) + \text{C}
Gracias por estar en este momento con nosotros : )