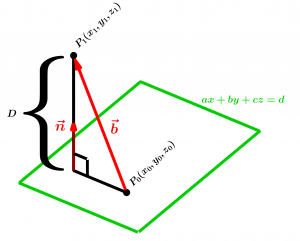
Comencemos representando el punto A y el plano ax + by + cz = d:
Sea el punto P_{1} en el plano dado. Del plano tenemos al punto P_{0} y además un vector \vec{b} que define al segmento \overset{\longrightarrow}{P_{0}P_{1}}:
\vec{b} = <x_{1} - x_{0},y_{1} - y_{0},z_{1} - z_{0} >
La distancia D de P_{1} al plano es igual al valor absoluto de la proyección escalar de \vec{b} sobre el vector normal \vec{n}:
D = \left| comp_{\vec{n}}\vec{b}\right| = \left| \cfrac{\vec{n}\cdot \vec{b}}{|\vec{n}|} \right|
La ecuación anterior se lee como el valor absoluto del producto punto del vector normal n por el vector b sobre el valor absoluto del vector normal n. Recuerda que el vector normal n se representa con los coeficientes de las incógnitas de la ecuación del plano respectivamente, eso quiere decir que si la ecuación del plano es ax + by + cz = d, entonces el vector normal es \vec{n} = <a,b,c>. Aquí tienes la ecuación obtenida de las operaciones de la ecuación anterior:
D =\cfrac{a(x_{1} - x_{0}) + b(y_{1} - y_{0}) + c(z_{1} - z_{0})}{\sqrt{a^{2} + b^{2} + c^{2}}}
Multiplicando los paréntesis queda de la siguiente manera:
D =\cfrac{ax_{1} - ax_{0} + by_{1} - by_{0} + cz_{1} - cz_{0}}{\sqrt{a^{2} + b^{2} + c^{2}}}
Ordenamos todas las incógnitas con subíndice 1 juntas y las incógnitas con subíndice 0 juntas:
D =\cfrac{ax_{1} + by_{1} + cz_{1} - ax_{0} - by_{0} - cz_{0}}{\sqrt{a^{2} + b^{2} + c^{2}}}
Factorizamos el negativo y queda de la siguiente forma:
D =\cfrac{ax_{1} + by_{1} + cz_{1} - (ax_{0} + by_{0} + cz_{0})}{\sqrt{a^{2} + b^{2} + c^{2}}}
Pero como la ecuación general del plano es:
a(x - x_{0}) + b(y - y_{0}) + c(z - z_{0}) = 0
ax - ax_{0} + by - by_{0} + cz - cz_{0} = 0
ax + by + cz = ax_{0} + by_{0} + cz_{0}
Observamos que d = ax_{0} + by_{0} + cz_{0}, entonces la ecuación de la distancia del punto al plano se puede escribir finalmente de la siguiente manera:
D = \cfrac{ax_{1} + by_{1} + cz_{1} - d}{\sqrt{a^{2} + b^{2} + c^{2}}}
Ejercicio de distancia entre un punto y un plano
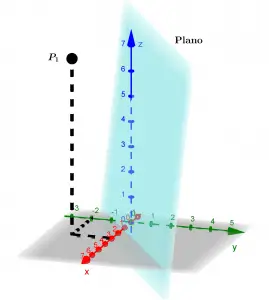
Halle la distancia del punto (3,-2,7) al plano 4x - 6y + z = 5
No es necesario graficar el punto y el plano, pero lo vamos a hacer:
El ejercicio se resuelve en un simple formulazo, tenemos P_{1} que es:
P_{1} = (3,-2,7)
El vector normal es el que nos dará los valores de a, b y c; pero el vector normal son los coeficientes de las incógnitas de la ecuación del plano respectivamente:
\begin{array}{c c c c c c} \vec{n} & = < & 4, & -6, & 1 & >\\ & & a & b & c & \end{array}Con nuestro punto P_{1}, nuestro vector normal y d, simplemente sustituimos en la fórmula:
D = \cfrac{(4)(3) + (-6)(-2) + (1)(7) - 5}{\sqrt{(4)^{2} + (-6)^{2} + (1)^{2}}}
Y agarramos una calculadora para hacer más fácil las operaciones de la fórmula para finalmente tener nuestra distancia entre el punto P_{1} y el plano:
D = \cfrac{26\sqrt{53}}{53} \ \text{u}
La \text{u} significa “unidades”.
Gracias por estar en este momento con nosotros : )