La distancia entre planos paralelos es un concepto sencillo del cual vamos a redactar su fórmula y veremos un ejemplo.
Fórmula de distancia entre planos paralelos
Vamos a redactar las ecuaciones de los siguientes planos paralelos para poder redactar la fórmula:
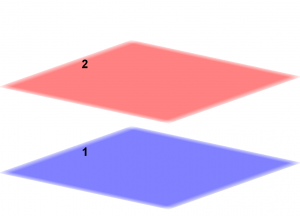La peculiaridad que tienen los planos paralelos es que en los coeficientes de las incógnitas x, y y z van a tener el mismo valor y lo único que tienen de diferente es el valor del término independiente, observemos la ecuación del plano 1 y del plano 2 respectivamente:
ax + by + cz = d_{1}
ax + by + cz = d_{2}
Una vez que ya hemos comprendido que el término independiente es lo único que cambia, vamos a mostrar la fórmula para calcular la distancia de los planos paralelos:
D = \cfrac{\left| d_{2} - d_{1}\right|}{\sqrt{a^{2} + b^{2} + c^{2}}}
Ejemplo de distancia entre planos paralelos
Calcular la distancia entre los planos:
(1) \ \ x + y + z = 4
(2) \ \ 2x + 2y + 2z = 6
Como se puede apreciar, los coeficiente de las incógnitas no tienen los mismos valores, así que para solucionar esto podemos multiplicar por 2 la ecuación 1 o podemos dividir entre 2 la ecuación 2. Lo que haremos será dividir entre 2 la ecuación 2 para hacer más rápido los cálculos:
(1) \ \ x + y + z = 4 \quad \quad \quad (2) \ \ x + y + z = 3
Una vez que ya tienen los mismos coeficientes, podemos aplicar la fórmula:
D = \cfrac{\left| d_{2} - d_{1}\right|}{\sqrt{a^{2} + b^{2} + c^{2}}} = \cfrac{\left| 3-4\right|}{\sqrt{1^{2} + 1^{2} + 1^{2}}}
D = \cfrac{1}{\sqrt{3}} = \cfrac{\sqrt{3}}{3}
Así que la distancia que hay entre los planos paralelos 1 y 2 es:
D = \cfrac{\sqrt{3}}{3}
Gracias por estar en este momento con nosotros : )
