Dos insectos se arrastran a lo largo de rectas diferentes en el espacio. En el instante t (en minutos), la catarina está en el punto (x, y, z) sobre la recta x=6+t, y=8-t, z=3+t, también en ese instante t, la hormiga está en el punto (x, y, z) sobre la recta x= 1+t, y=2+t, z=2t.
a) Halla la distancia entre los insectos en el instante en que t=0
Para este inciso lo que haremos es bastante sencillo, simplemente sustituiremos las t de cada insecto:
\begin{array}{l} \text{Catarina} \\ x = 6 + (0) = 6 \\ y = 8 - (0) = 8 \\ z = 3 + (0) = 3\end{array}\begin{array}{l} \text{Hormiga} \\ x = 1 + (0) = 1 \\ y = 2 + (0) = 2 \\ z = 2(0) = 0 \end{array}Ahora tenemos que hallar el vector unido de la hormiga y la catarina, para eso simplemente hacemos lo siguiente:
\vec{PQ} = <6-1, 8-2, 3-0> = <5, 6, 3>
Calculamos el determinante del vector que une a los dos insectos:
\left| \vec{PQ} \right| = \sqrt{(5)^{2} + (6)^{2} + (3)^{2}} = \sqrt{25 + 36 + 9} = \sqrt{70}
Así que tenemos que la distancia de nuestros insectos en el tiempo t=0 es igual a \sqrt{70} unidades o aproximadamente 8.36 unidades.
b) Representar gráficamente la distancia de los insectos desde t=0 hasta t=10
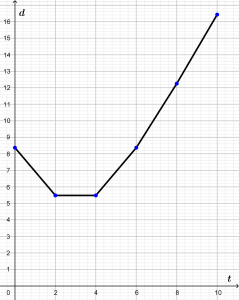
c) Usando la gráfica, ¿qué se puede decir acerca de la distancia entre los insectos?
Que su distancia nunca es cero, lo que quiere decir que nunca se encuentran.
d) ¿Qué tanto se acercan los insectos?
Para la resolución de este ejercicio tenemos que implementar la fórmula de distancia para nuestros amigos insectos, esta fórmula necesita el valor absoluto de los vectores de cada insecto y luego necesitamos el vector PQ para poder usarla en nuestra determinante.
Para empezar, tenemos que nuestro vector de la Catarina es el siguiente:
\vec{v_{C}}=<1,-1,1>
Y tenemos nuestro vector de la Hormiga que es:
\vec{v_{H}}=<1,1,2>
Para determinar nuestro vector de la Catarina y la Hormiga tenemos qué hacer una resta:
\vec{PQ} = <6-1, 8-2, 3-0> = <5, 6, 3>
Ahora lo que tenemos qué hacer es obtener nuestro determinante de nuestros vectores, para ello haremos lo siguiente:
\text{det}_{\text{v}}= \left| \begin{array}{c c c} 1 & -1 & 1 \\ 1 & 1 & 2 \\ 5 & 6 & 3 \end{array} \right|Y lo que haremos es copiar y pegar las primeras dos columnas para tener una mejor representación visual de las multiplicaciones:
\text{det}_{\text{v}}= \left| \begin{array}{c c c} 1 & -1 & 1 \\ 1 & 1 & 2 \\ 5 & 6 & 3 \end{array} \right|
\begin{array}{c c} 1 & -1 \\ 1 & 1 \\ 5 & 6 \end{array}Ahora escribimos las multiplicaciones:
\text{det}_{\text{v}}=(1\times 1 \times 3) + (-1\times 2 \times 5) + (1 \times 1 \times 6)
- [(5 \times 1 \times 1)+(6 \times 2 \times 1)+(3 \times 1 \times (-1))]
Y simplemente resolvemos las operaciones:
\text{det}_{\text{v}} = 3-10+6-[5+12-3]
\text{det}_{\text{v}} = -1-[14] = -1 -14 = -15
Ahora tenemos que obtener el determinante de nuestros vectores en i, j y k de la catarina y la hormiga, para eso haremos lo siguiente:
\left| u\times v\right| = \begin{Vmatrix} i & j & k \\ 1 & -1 & 1 \\ 1 & 1 & 2 \end{Vmatrix}Y para tener una mejor representación gráfica aplicaremos lo mismo del determinante anterior de copiar las primeras dos columnas:
\left| u\times v\right| = \begin{Vmatrix} i & j & k \\ 1 & -1 & 1 \\ 1 & 1 & 2 \end{Vmatrix} \begin{array}{c c} i & j \\ 1 & -1 \\ 1 & 1 \end{array}Ahora procederemos a multiplicar paso por paro todo el determinante:
\left| u\times v\right| = (i\times(-1)\times 2)+(j\times (1) \times (1) )+(k \times (1) \times (1))
- [((1) \times (-1) \times k)+((1) \times (1) \times i)+((2) \times (1) \times j)]
Reduciendo términos tenemos lo siguiente:
\left| u\times v\right| = -2i +j + k - [-k + i + 2j] = -2i+j+k+k-i-2j = -3i-j+2k
Y para calcular nuestro determinante de la intersección de los vectores de la hormiga y la catarina, se hace lo siguiente:
\left| u\times v\right| = \sqrt{(-3)^{2} + (-1)^{2} + (2)^{2}} = \sqrt{9+1+4} = \sqrt{14}
Perfecto, ¡ya tenemos nuestra intersección de los vectores de la hormiga y la catarina!
Ahora aplicaremos la fórmula de la distancia:
d = \cfrac{|\text{det}_{u}|}{|u\times v|} = \cfrac{|-15|}{\sqrt{14}} = \cfrac{15\sqrt{14}}{14}
Y listo, ya tenemos el valor de lo tanto que se acercan la hormiga y la catarina que es \frac{15\sqrt{14}}{14} o que es aproximadamente 4.0089 unidades.
Gracias por estar en este momento con nosotros : )
