En este post aprenderemos a cómo calcular el área de una función con valor absoluto. Es mucho más fácil de lo que parece.
Comencemos
Para la función f(x) = |x^{3} - x| calcula el área bajo la curva que se encuentra entre los límites de x = -1 y x = 1.
Hay que tener un poco de maña con esto de las funciones, recordemos que queremos calcular el área de la función f(x), pero descomponer f(x) en dos funciones como: 1. x^{3} - x y 2. x - x^{3} no es suficiente si no se sabe cómo se comportan.
Calculemos los puntos de intersección de la función f(x). Igualemos a cero:
x^{3} - x = 0
Factorizaremos una sola x:
x(x^{2} - 1) = 0
Ahora factorizaremos el binomio:
x(x + 1)(x - 1) = 0
Y lo que podemos observar es que los puntos de intersección son cuando x = -1, x = 0 y x = 1, con esto ya hasta podríamos plantear nuestra integral, sólo faltan unas cosas más.
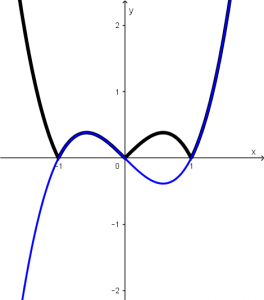
Descomponiendo la función f(x), la primera función obtenida que es x^{3} - x la pintamos de azul y se visualizará de la siguiente manera:
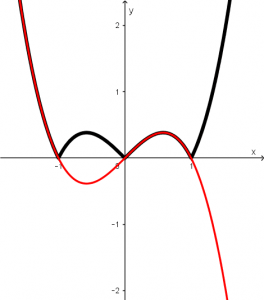
Y la segunda función obtenida que es x - x^{3} la pintamos de rojo y se visualizará de la siguiente manera:
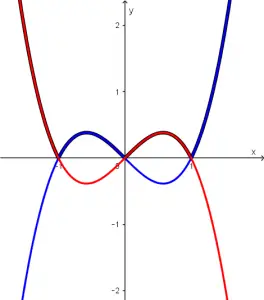
Si juntamos las dos funciones en una misma gráfica obtendremos lo siguiente:
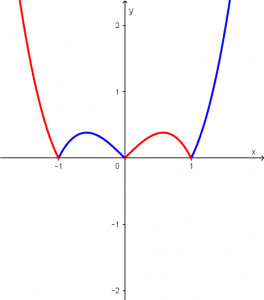
Bien bien, pero por lo que se observa, no necesitamos toda la función, necesitamos una parte de cada una de las funciones. Vamos a quitar la gráfica original que es la de color negro y dejaremos sólo las partes que representan a nuestra gráfica original con las partes que intersecan a nuestras funciones roja y azul:
¡Genial! Eso que acabamos de representar se puede escribir matemáticamente gracias a que calculamos los puntos de intersección de la función original f(x) y una vez que lo escribamos ya sabremos cómo realizar nuestra integral para el cálculo del área. Matemáticamente es así:
f(x) = \left\{ \begin{array}{l l l}
x^{3} - x \quad & \text{ cuando } \quad & x \in [-1,0] \cup [1,\infty] \\
x - x^{3} & \text{ cuando } & x \in [-\infty,-1] \cup [0,1]
\end{array}\right.Aprovechando la simetría de la función, podemos realizar una integral que vaya de 0 a 1 y el resultado multiplicarlo por 2, veamos:
\displaystyle A = \int_{0}^{1}(x - x^{3}) \ dx
La integral de x es \frac{x^{2}}{2} y la integral de x^{3} es \frac{x^{4}}{4}:
A = \left. \cfrac{x^{2}}{2} - \cfrac{x^{4}}{4} \right]_{0}^{1}
Evaluamos:
A = \cfrac{1}{2} - \cfrac{1}{4} - 0 = \cfrac{1}{4}
Ahora ese resultado obtenido lo multiplicaremos por 2 para obtener el área total:
A = \cfrac{1}{4}(2) = \cfrac{1}{2} \ \text{u}^{2}
Así que el área total de la función |x^{3} - x| entre los límites de x = -1 a x = 1 es igual a \frac{1}{2} \ \text{u}^{2}
Gracias por estar en este momento con nosotros : )