Como primer ejercicio, vamos a empezar con algo “complejo”. Calcularemos el área entre las siguientes funciones:
- x=3 - y^{2}
- y = x - 1
Lo primero que se recomienda es tratar de bosquejar las gráficas para tener una mejor idea de cómo vamos a trabajar. Si es posible, utiliza alguna herramienta de graficación como la de GeoGebra.
Las funciones graficadas en el programa se verán de la siguiente manera:
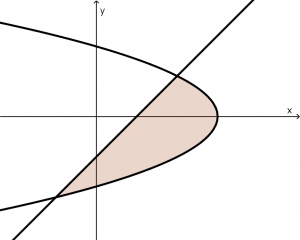
Y el área sombreada que se visualiza entre las funciones es la que se calculará en este ejercicio.
Primero vamos a calcular la intersección entre curvas, este cálculo es importante porque es el que nos definirá los límites de nuestras integrales. Para hacer este cálculo tomaremos la función 1 y su incógnita de y la sustituiremos por la función 2, matemáticamente es así:
x = 3 - y^{2}
x = 3 - (x - 1)^{2}
Ahora que ya tenemos una ecuación con un sólo tipo de incógnita, procedamos a igualarla a cero para hallar los valores de x en los que se intersecan las funciones, elevemos al cuadrado el binomio:
x = 3 - (x^{2} - 2x + 1)
Multipliquemos ese signo negativo a todo el paréntesis:
x = 3 - x^{2} + 2x - 1
Ahora vamos a igualar a cero:
x^{2} - x - 2 = 0
Una vez que ya tenemos la ecuación cuadrática lo más reducida posible, vamos a factorizarla para obtener los valores de x:
(x - 2)(x + 1) = 0
Lo que nos da como resultado que hay un punto que tiene el valor de x = 2 y el otro punto tiene el valor de x = -1.
Fácilmente podemos hallar los valores de y de cada punto utilizando la función 2 que es más sencilla de hacer cálculos que la función 1. Sólo tenemos que sustituir cada valor obtenidos de x:
Cuando x = -1
y = x - 1 \ \rightarrow \ y = -1 - 1 = -2
Cuando x = 2
y = x - 1 \ \rightarrow \ y = 2 - 1 = 1
Así que nuestros puntos de intersección entre las dos funciones son (-1,-2) y (2,1)
Con haber hallado el valor de x era más que suficiente, sólo que como igual vamos a calcular el área tomando como referencia al eje de las ordenadas, calculamos las y‘s.
Un punto que no hemos calculado que es muy importante es el vértice de la parábola de la función 1, para calcularlo sólo se tiene que igualar a cero el valor de y y ya tendremos el valor de x:
x = 3 - y^{2} = 3 - (0)^{2} = 3
Sólo falta separar la función 1, vamos a ponerla como una función f(x), la parte de la función que está por arriba de la abscisa quedará de la siguiente manera:
y = \sqrt{3 - x}
Y la parte de la función que está por debajo de la abscisa quedará así:
y = - \sqrt{3 - x}
Todo lo que acabamos de calcular de puntos de intersecciones y la función 1 que tuvimos que separarla en dos funciones, lo representaremos en la siguiente imagen:
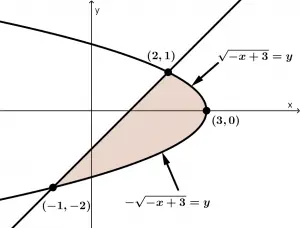
Comencemos con las integrales
Esto funciona así, vamos a necesitar dos integrales y lo que se va a integrar va a ser la función que está más arriba menos la función que está más abajo del área que se quiere hallar. Nuestra primer integral va a tener límites de -1 a 2:
\displaystyle \int_{-1}^{2} \left[ (x - 1) - \left( -\sqrt{-x + 3} \right)\right] dx
Y nuestra segunda integral va a tener límites de 2 a 3:
\displaystyle \int_{2}^{3} \left[ \left(\sqrt{-x + 3} \right) - \left( -\sqrt{-x+3} \right) \right] dx
Así que nuestra área se calcula con la suma de las dos integrales planteadas:
\displaystyle A = \int_{-1}^{2} \left[ (x - 1) - \left( -\sqrt{-x + 3} \right)\right] dx + \int_{2}^{3} \left[ \left(\sqrt{-x + 3} \right) - \left( -\sqrt{-x+3} \right) \right] dx
Puedes utilizar una calculadora para obtener rápidamente el valor de las integrales, sólo que aquí explicaremos paso a paso la resolución de las integrales.
Reduzcamos los paréntesis de las integrales:
\displaystyle A = \int_{-1}^{2} \left[ (x - 1) + \sqrt{-x + 3} \right] dx + \int_{2}^{3} \left[ \sqrt{-x + 3} + \sqrt{-x+3} \right] dx
Sumamos las dos raíces de la segunda integral y por propiedades de las integrales podemos sacar el 2 de la integral:
\displaystyle A = \int_{-1}^{2} \left[ (x - 1) + \sqrt{-x + 3} \right] dx + 2\int_{2}^{3} \left[ \sqrt{-x + 3}\right] dx
Fácilmente podemos efectuar las integrales. Integral de x es igual a \frac{x^{2}}{2}, integral de una constante es igual a la constante multiplicada por x y para realizar la integral de la raíz cuadrada tenemos que aplicar regla de la cadena que dará como resultado que integral de \sqrt{-x+3} es igual a \frac{2}{3}\left( -x + 3 \right)^{\frac{3}{2}}. La segunda integral se aplica la regla de la cadena y al \frac{2}{3} lo multiplicaremos por el 2 que está fuera de la integral, lo que dará como resultado un -\frac{4}{3}:
A = \left[ \cfrac{x^{2}}{2} - x - \cfrac{2}{3} \left(-x + 3 \right)^{\frac{3}{2}}\right]_{-1}^{2} + \left[-\cfrac{4}{3} \left(-x + 3\right)^{\frac{3}{2}} \right]_{2}^{3}
Evaluaremos con sus respectivos límites:
A = \left[ \left(2 - 2 - \cfrac{2}{3} \right) - \left( \cfrac{1}{2} + 1 - \cfrac{16}{3} \right) \right] + \left[ 0 + \cfrac{4}{3} \right] = \cfrac{9}{2} \ \text{u}^{2}
Lo que nos da como resultado que el área entre las dos funciones es igual a \frac{9}{2} \ \text{u}^{2}
Cambiemos de sistema de referencia
Tomaremos como sistema de referencia al eje de las ordenadas.
Parecerá que es más difícil, pero la verdad es que es más fácil y rápido de calcular este ejercicio cuando tomamos como sistema de referencia al de las ordenadas. Se van a hacer los mismo pasos, sólo que con este sistema de referencia sólo vamos a plantear una integral. Los límites son los puntos de intersección que ya los habíamos calculado y lo que se integrará será la función que está más arriba (la que está más a la derecha) menos la función que está más abajo (la que está más a la izquierda) del área que se quiere calcular. Veamos:
\displaystyle A = \int_{-2}^{1} \left[ \left(3 - y^{2} \right) - \left(y + 1\right) \right] \ dy
Simplificamos los paréntesis que tiene la integral:
\displaystyle A = \int_{-2}^{1} \left[ 2 - y^{2} - y \right] \ dy
Integral de una constante es igual a la constante por y, la integral de y^{2} es igual a \frac{y^{3}}{3} e integral de y es igual a \frac{y^{2}}{2}:
A = \left[2y - \cfrac{y^{3}}{3} - \cfrac{y^{2}}{2} \right]_{-2}^{1}
Sólo falta evaluar y casi habremos terminado:
\left( 2 - \left(\cfrac{1}{3} \right) - \left( \cfrac{1}{2} \right) \right) - \left( - 4 + \left(\cfrac{8}{3} \right) - (2) \right) = \cfrac{9}{2} \ \text{u}^{2}
Finalmente nuestra área calculada es igual a \frac{9}{2} \ \text{u}^{2}
Lo que se demostró es que se puede calcular el mismo área tomando sistemas de referencia diferente e incluso puede resultar mucho más fácil un sistema de referencia que el otro, al final es decisión de cada uno usar el sistema de referencia que quiera, lo que importa es obtener el resultado correcto.
Gracias por estar con nosotros en este momento : )
