▷ Operaciones con Números Complejos

A continuación explicaremos las operaciones fundamentales con números complejos como la suma, resta, multiplicación, división, potenciación y raíces, se será lo más explícito posible y hasta incluiremos ejemplos de operaciones con números complejos. Antes de comenzar, recuerda que el valor de $i = \sqrt{-1}$

Suma de números complejos

Para sumar números complejos, se suman por separado todas las partes reales de las imaginarias.

Ejemplo de suma de números complejos

$(2 + 3i)+(4 - 7i)$

Eliminemos los paréntesis

$2 + 3i + 4 - 7i$

Y ahora sumemos los números reales y los números imaginarios

$2 + 4 + 3i - 7i = 6 - 4i$

Resta de números complejos

Para restar números complejos, se restan por separado todas las partes reales de las imaginarias.

Ejemplo de resta de números complejos

$(2 + 3i)-(4 - 7i)$

Eliminemos los paréntesis

$2 + 3i - 4 + 7i$

Y ahora sumemos los números reales y los números imaginarios

$2 - 4 + 3i + 7i = -2 + 10i$

Multiplicación de números complejos

El producto de números complejos se obtiene multiplicándose como binomios comunes, las operaciones posteriores después de reducir términos dependerán del exponente al que se encuentre $i$ .

Ejemplo del producto de números complejos

$(2 + 3i)(4 - 7i)$

Procedemos a realizar la multiplicación paso por paso:

$2(4) - 2(7i) + 4(3i) - (3i)(7i)$

$8 - 14i + 12i - 21i^{2}$

Ahora, reduciremos términos semejantes, sumaremos los términos de $i$ :

$8 - 2i - 21i^{2}$

Recordando el valor de $i = \sqrt{-1}$ , podemos decir que $i^{2} = \left( \sqrt{-1}\right)^{2} = -1$ , así que sustituyamos ese término:

$8 - 2i - 21(-1) = 8 - 2i + 21$

Finalmente obtendremos que el producto de los números complejos es:

$29 - 2i$

División de números complejos

Para realizar la división de números complejos, se tiene que utilizar la racionalización ya que lo que se quiere es eliminar los números imaginarios que se encuentren en el denominador ya que no es práctico o correcto que haya números complejos en el denominador.

Ejemplo de la división de números complejos

$\cfrac{2 + 3i}{4 - 7i}$

Para racionalizar vamos a multiplicar la fracción por otra fracción del conjugado del denominador, observa lo siguiente:

$\cfrac{2 + 3i}{4 - 7i} \cdot \cfrac{4 + 7i}{4 + 7i}$

Se observa que en el denominador tenemos binomios conjugados, así que procedamos paso a paso a efectuar las operaciones tanto en el denominador como en el numerador:

$\cfrac{2 + 3i}{4 - 7i} \cdot \cfrac{4 + 7i}{4 + 7i} = \cfrac{2(4) + 2(7i) + 4(3i) + (3i)(7i)}{(4)^{2} - (7i)^{2}}$

$\cfrac{8 + 14i + 12i + 21i^{2}}{16 - 49i^{2}}$

Recordemos que el valor de $i^{2} = \left( \sqrt{-1}\right)^{2} = -1$ , así que procedamos a sustituir ese término en las $i^{2}$ de la fracción que estamos resolviendo e igual reduzcamos términos:

$\cfrac{8 + 26i + 21(-1)}{16 - 49(-1)}= \cfrac{8 + 26i - 21}{16 + 49}$

$\cfrac{8 - 21 + 26i}{65} = \cfrac{-13 + 26i}{65}$

Como paso final podemos separar la fracción:

$\cfrac{-13}{65} + \cfrac{26}{65}i$

$= \cfrac{-1}{5} + \cfrac{2}{5} i$

Potencias de números complejos

Hay un teorema muy poderoso de los números imaginarios que nos ahorrará mucho trabajo, hay que tenerlo en cuenta porque sí es bastante útil, dice así:

El módulo del producto de dos números complejos es igual al producto de sus módulos y el argumento del producto es igual a la suma de los argumentos.

Ahora, con el teorema bien claro, si tenemos dos números complejos iguales, su producto está dado por la siguiente relación:

$\left( x + yi \right)^{2} = \left[r\left( \cos \theta + i \sin \theta \right) \right]^{2} = r^{2} \left( \cos 2 \theta + i \sin 2 \theta \right)$

$\left(x + yi \right)^{3} = \left[r\left( \cos \theta + i \sin \theta \right) \right]^{3} = r^{3} \left( \cos 3 \theta + i \sin 3 \theta \right)$

$\left(x + yi \right)^{4} = \left[r\left( \cos \theta + i \sin \theta \right) \right]^{4} = r^{4} \left( \cos 4 \theta + i \sin 4 \theta \right)$

Sin importar el exponente que tenga, siempre se va a cumplir, lo que nos da como resultado el siguiente teorema, que es mejor conocido como el Teorema de De Moivre:

$\left( x + yi \right)^{n} = \left[r\left( \cos \theta + i \sin \theta \right) \right]^{n} = r^{n} \left( \cos n \theta + i \sin n \theta \right)$

Ejemplo de la potencia de números complejos

Reduce el siguiente número complejo $\left( 2 - 2i\right)^{10}$ , se te recomienda que primero lo grafiques.

Figura 1.

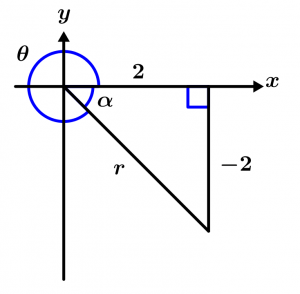
Para poder resolver el número complejo, lo primero que tenemos que hacer es hallar su módulo y su argumento, vamos a hallar primero su módulo:

$x = 2 \qquad y = -2$

Recordando que $r = \sqrt{x^{2} + y^{2}}$ tenemos lo siguiente:

$r = \sqrt{(2)^{2} + (-2)^{2}} = \sqrt{4 + 4} = \sqrt{8}$

$r = 2\sqrt{2}$

Ahora calculemos el argumento de nuestro número complejo:

Recordando que $\tan \alpha = \cfrac{y}{x}$ tenemos lo siguiente:

$\tan \alpha = \cfrac{-2}{2}$

Por el momento podemos ignorar el signo, ya después lo acomodaremos con respecto al cuadrante donde se encuentra:

$\tan \alpha = \cfrac{2}{2} = 1$

$\alpha = \tan^{-1}(1) = 45°$

Cabe recalcar que el ángulo que se halla con la tangente inversa sólo es el ángulo de elevación del módulo medido desde el ángulo más corto en el eje $x$ , el ángulo $\theta$ tiene un valor entre $0° \le \theta \le 360°$ y en este caso el ángulo $\theta$ tiene un valor de $360° - \alpha = 315°$ .

Así que una vez que ya tenemos el argumento y el módulo, podemos proceder a sustituir en la ecuación del Teorema de De Moivre:

$\left[r\left( \cos \theta + i \sin \theta \right) \right]^{n} =$

$\left(2\sqrt{2} \right)^{10}\left[ \cos 10(315°) + i \sin 10 (315°) \right]$

Procedemos a elevar a la diez al $2\sqrt{2}$ y multiplicaremos $10(315°)$ :

$32768\left[ \cos 3150° + i \sin 3150°\right]$

Ahora, ¿cómo resolvemos las funciones trigonométricas con ese ángulo de $3150°$ ? A partir de aquí hay un concepto que me gusta emplear, que es el número de vueltas haciendo una simple regla de 3. Para esos ángulos muy grandes, el valor que obtengamos en la regla de 3 le quitaremos la parte entera y sólo nos quedaremos con los decimales para hallar el ángulo. Mira, si $1 \ \text{vuelta}$ equivale a $360°$ , ¿a cuántas vueltas $v$ equivale $3150°$ ?

\begin{array}{c c c} 1 \ \text{vuelta} & \ \Rightarrow \ & 360° \\ v & \ \Rightarrow \ & 3150° \end{array}

Ahora efectuando nuestra simple regla de 3, obtendremos lo siguiente:

$v = \cfrac{3150(1)}{360} = \cfrac{35}{4} = 8.75$

Así que $3150°$ equivale a $8.75$ vueltas, ahora le tenemos que quitar la parte entera y volver a hacer una regla de 3. Si una vuelta equivale a $360°$ , ¿a cuántos grados $g_{1}$ equivale $0.75$ vueltas?

\begin{array}{c c c} 1 \ \text{vuelta} & \ \Rightarrow \ & 360° \\ 0.75 & \ \Rightarrow \ & g_{1} \end{array}

Efectuando nuestra regla de 3 obtendremos lo siguiente:

$g_{1} = \cfrac{0.75(360°)}{1} = 270°$

Genial, con este nuevo valor de ángulo hallado podemos proceder a sustituirlo, cambiaremos $3150°$ con $270°$ que es exactamente lo mismo al momento de aplicar seno y coseno:

$32768\left[ \cos 270° + i \sin 270° \right]$

Observa la figura 2:

Figura 2.

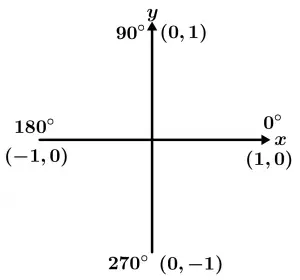
Como el ángulo de $270°$ se encuentra en uno de los ejes, el valor de esas “hipotenusas” es del valor de $1$ (porque se supone que los 3 lados del “triángulo” miden lo mismo ya que “están” los 3 lados en el mismo eje de $270°$ ). Ahora, esto deja en claro que $\sin = \frac{y}{h}$ y que $\cos \frac{x}{h}$ y que lo que vemos en la figura 2 en el ángulo de $270°$ es que la coordenada que tiene es de $(0,-1)$ , lo que quiere decir que el valor de $x$ es cero y que el valor de $y$ es $-1$ , así que:

$\sin 270° = \cfrac{y}{h} \qquad \cos 270° = \cfrac{x}{h}$

$\sin 270° = \cfrac{-1}{1} = -1 \qquad \cos 270° = \cfrac{0}{1}$

$\sin 270° = -1 \qquad \cos 270° = 0$

Una vez que ya tengamos esos valores hallados, podemos proceder a continuar:

$32768\left[ \cos 270 + i \sin 270 \right] = 32768 \left[0 + i (-1) \right]$

$32768 \left[ -i\right]$

Ahora sólo efectuamos una última multiplicación para obtener que:

$-32768i$

¡Así que nuestro número complejo de $\left(2 - 2i\right)^{10}$ desarrollado es igual a $-32768i$ !

Raíces de números complejos

Para que se tenga el dominio total del las raíces de números complejos, le súper recomiendo consultar el libro de Lehmann, C., (2012). Álgebra. México, DF, México: Editorial Limusa. en la parte de “Potencias y raíces” o en las páginas 185-187.

Pero te voy a dejar un resumen a continuación, necesitarás el siguiente teorema que viene en la página 186 del Lehmann:

Todo número (excepto el cero), real o complejo, tiene exactamente $n$ raíces enésimas diferentes.

Si el módulo y el argumento de un número cualquiera se representan con $r$ y $\theta$ , respectivamente, entonces las $n$ raíces están dadas por la expresión:

$r^{\frac{1}{n}} \left[ \cos \cfrac{\theta + k \cdot 360°}{n} + i \sin \cfrac{\theta + k \cdot 360°}{n} \right]$

Y si se pide que se calculen las raíces cuartas, las cuatro raíces o las raíces $n=4$ , $k$ tiene que ir del valor $0$ al $3$ , eso quiere decir que el valor de $k$ va a ir de cero hasta $n-1$ .

Ejemplo de las raíces de números complejos

Hallar las $n=5$ raíces de $\left(-\sqrt{24} - \sqrt{8}i\right)$

$x = -\sqrt{24} \qquad y = -\sqrt{8}$

Figura 3.

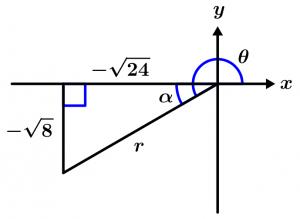
Nota: En estos ejemplos de raíces de números imaginarios sí es recomendable utilizar una calculadora para hacer más óptimo el tiempo de hacer cálculos.

Para proceder con la resolución, primero tenemos que hallar la forma polar de nuestro número complejo, calculamos el módulo:

$r = \sqrt{x^{2} + y^{2}} = \sqrt{(-\sqrt{24})^{2} + (-\sqrt{8})^{2}}$

$r = \sqrt{32} = 4\sqrt{2}$

Ahora hay que calcular el argumento, primero calculemos el ángulo de elevación que tiene el módulo ignorando los signos de $x$ y $y$ :

$\tan \alpha = \cfrac{y}{x} = \cfrac{\sqrt{8}}{\sqrt{24}}$

$\alpha = \tan^{-1}\cfrac{\sqrt{8}}{\sqrt{24}} = 30°$

Con el valor de $\alpha$ ya podemos saber el valor del argumento que es $\theta = 180°+ \alpha = 210°$

Genial, ahora que ya tenemos el argumento, podemos sustituir términos en la fórmula vista en el teorema de esta sección:

$r^{\frac{1}{n}} \left[ \cos \cfrac{\theta + k \cdot 360°}{n} + i \sin \cfrac{\theta + k \cdot 360°}{n} \right] =$

$\left( \sqrt{32} \right)^{\frac{1}{5}} \left[ \cos \cfrac{210° + k \cdot 360°}{5} + i \sin \cfrac{210° + k \cdot 360°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + k \cdot 360°}{5} + i \sin \cfrac{210° + k \cdot 360°}{5} \right]$

Sólo falta sustituir las $k$ por $0,1,2,3$ y $4$ , te súper recomiendo que utilices la calculadora y recuerda colocarla en GRADOS, debe de marcar una D arriba encerrada en un cuadrado $\fbox{D}$ , así que nuestras 5 raíces son las siguientes:

k=0

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + 0 \cdot 360°}{5} + i \sin \cfrac{210° + 0 \cdot 360°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210°}{5} + i \sin \cfrac{210°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos 42° + i \sin 42° \right]=$

$\left( \sqrt{2} \right) \left[ 0.74 + i 0.67 \right]$

$0.74\sqrt{2} + 0.67\sqrt{2}i$

k=1

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + 1 \cdot 360°}{5} + i \sin \cfrac{210° + 1 \cdot 360°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + 360°}{5} + i \sin \cfrac{210° + 360°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{570°}{5} + i \sin \cfrac{570°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos 114° + i \sin 114° \right]=$

$\left( \sqrt{2} \right) \left[ -0.40 + 0.91i \right]=$

$-0.40\sqrt{2} + 0.91\sqrt{2}i$

k=2

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + 2 \cdot 360°}{5} + i \sin \cfrac{210° + 2 \cdot 360°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + 720°}{5} + i \sin \cfrac{210° + 720°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{930°}{5} + i \sin \cfrac{930°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos 186° + i \sin 186° \right]=$

$\left( \sqrt{2} \right) \left[ -0.99 - 0.10i \right]=$

$-0.99\sqrt{2} - 0.10\sqrt{2}i$

k=3

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + 3 \cdot 360°}{5} + i \sin \cfrac{210° + 3 \cdot 360°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + 1080°}{5} + i \sin \cfrac{210° + 1080°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{1290°}{5} + i \sin \cfrac{1290°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos 258° + i \sin 258° \right]=$

$\left( \sqrt{2} \right) \left[ -0.20 - 0.97i \right]=$

$-0.20\sqrt{2} - 0.97\sqrt{2}i$

k=4

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + 4 \cdot 360°}{5} + i \sin \cfrac{210° + 4 \cdot 360°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{210° + 1440°}{5} + i \sin \cfrac{210° + 1440°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos \cfrac{1650°}{5} + i \sin \cfrac{1650°}{5} \right]=$

$\left( \sqrt{2} \right) \left[ \cos 330° + i \sin 330° \right]=$

$\left( \sqrt{2} \right) \left[ \cfrac{\sqrt{3}}{2} - \cfrac{1}{2}i \right]=$

$\cfrac{\sqrt{3}}{2}\sqrt{2} - \cfrac{1}{2}\sqrt{2}i$

$\cfrac{\sqrt{6}}{2} - \cfrac{\sqrt{2}}{2}i$

Gracias por estar en este momento con nosotros : )