La representación polar de un número complejo es también conocida como la forma trigonométrica de un número complejo, a continuación veremos la representación polar de P que es el número complejo x + yi:
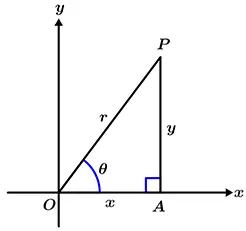
En el triángulo observado en la figura 1, se puede escribir todo lo siguiente:
x = r \cos \theta ,\qquad y = r \sin \theta
r = \sqrt{x^{2} + y^{2}}, \qquad r \ge 0
\tan \theta = \cfrac{y}{x}, \qquad x \neq 0
Con los datos mencionados, podemos escribir que:
x + yi = r \cos \theta + i \sin \theta = r\left( \cos \theta + i \sin \theta \right)
El miembro r\left(\cos \theta+ i \sin \theta \right) es lo que se conoce como la forma polar del número complejo x + yi.
Nota: Recuerda que el término de los reales forma parte del eje x de las abscisas y el término imaginario forma parte del eje y de las ordenadas.
Módulo de un número complejo
La letra r que se tiene en la ecuación polar del número complejo es la que se conoce como módulo del número complejo. También a este módulo r se le llama valor absoluto del número complejo y se puede escribir como r = \left|x + yi \right|
Argumento de un número completo
El ángulo \theta se le conoce como amplitud o argumento del número complejo y \theta quedará restringida al dominio de 0 \le \theta \le 360^{\text{o}} a menos que se especifique lo contrario en algún ejercicio.
Ejemplo de número complejo a forma polar
Vamos como sacar la forma polar de un numero complejo de forma rectangular a forma polar, para hacer eso tenemos que hallar el módulo y el argumento, además, es mejor representar los ejemplos gráficamente para que sea más claro, veamos el ejemplo, empecemos.
Vamos con el ejemplo
Hallar la forma polar de E_{1} = -2 + 2i
Siempre intentemos graficar nuestro número complejo para que sea más sencillo poder interpretar los datos que queremos hallar.
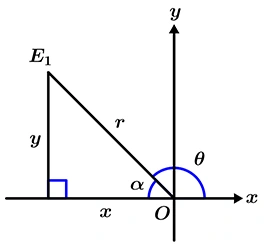
Hallemos el módulo de la siguiente manera:
x = -2 \qquad y = 2
r = \sqrt{x^{2} + y^{2}} = \sqrt{(-2)^{2} + (2)^{2}} = \sqrt{4 + 4} = \sqrt{8}
r = 2\sqrt{2}
Una vez que ya tenemos el módulo, hay que calcular el argumento, aquí haremos un pequeño truco donde \alpha representa al ángulo de elevación del módulo, para eso procedemos a realizar lo siguiente:
\tan \alpha = \cfrac{y}{x} = \cfrac{2}{-2} = -1
Ahora hay que aplicar tangente inversa a -1, puedes utilizar una calculadora si gustas:
\alpha = \tan^{-1}(-1) = -45^{\text{o}}
Pero con sólo calcular el ángulo no es suficiente, lo que se hace es ignorar el signo que tiene el ángulo calculado y sólo tomaremos el ángulo de elevación \alpha en el cuadrante en donde esté nuestro número imaginario, en este ejemplo, el punto E_{1} nos dice que estamos en el segundo cuadrante, así que el ángulo de elevación de la recta del módulo r mide 45°, el ángulo \theta se mide desde la línea positiva de las abscisas hasta la línea del módulo, observando la figura 3 se puede apreciar en dónde está ubicado \theta.
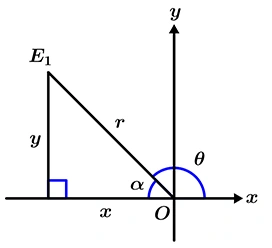
Así que resulta que \theta = 180° - \alpha = 135°
Una vez calculado el módulo y el argumento del número complejo, finalmente tenemos que la forma polar de -2 + 2i es:
2\sqrt{2} \left( \cos 135°+ i \sin 135° \right)
¿Cómo comprobamos que la forma polar de un número complejo hallada es correcta?
Te voy a ser sincero, la verdad es que es bastante sencillo de comprobar si nuestra forma polar del número imaginario es correcta, para este caso sólo necesitas un triángulo rectángulo como el de la figura 4.
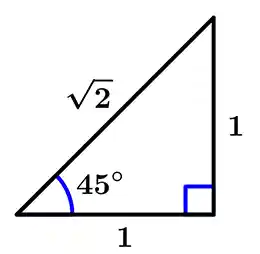
Ese triángulo sólo es para fines ilustrativos, los ajustes los haremos en la marcha.
Si no tienes calculadora (imagina que por el momento la guardaste y no quieres ir por ella) para calcular el valor de \cos 135°, puedes realizar el cálculo de -\cos 45° ya que dan exactamente el mismo resultado, el signo negativo se le agrega debido a que el ángulo se encuentra en el segundo cuadrante y como coseno hace representación a x (los números reales), si está en el segundo o tercer cuadrante, tomará valores negativo, con la práctica te darás cuenta de que lo puedes trabajar en el primer cuadrante por la facilidad de los signos positivos, pero debes de recordar que siempre hay que colocarle los signos dependiendo del cuadrante donde pertenezca el ángulo original. Bueno, continuemos, coseno es cateto adyacente sobre hipotenusa:
-\cos 45° = -\cfrac{1}{\sqrt{2}} = - \cfrac{\sqrt{2}}{2}
Genial, una vez que ya tengamos el valor de \cos 135°, vamos a hallar el valor de \sin 135°. Trabajando con nuestro triangulito de la figura 4, \sin 135° es igual a \sin 45°, y como seno es cateto opuesto sobre hipotenusa, tendremos lo siguiente:
\sin 45° = \cfrac{1}{\sqrt{2}} = \cfrac{\sqrt{2}}{2}
Una vez que ya tengamos los dos valores de \cos 135° y \sin 135°, vamos a sustituirlos en nuestra forma polar:
2\sqrt{2} \left( \cos 135° + i \sin 135°\right) = 2\sqrt{2} \left( -\cfrac{\sqrt{2}}{2} + i\cfrac{\sqrt{2}}{2} \right)
Multiplicamos el paréntesis para obtener lo siguiente:
2\sqrt{2} \left( -\cfrac{\sqrt{2}}{2} \right) + 2\sqrt{2}\left(\cfrac{\sqrt{2}}{2} \right)i
Efectuando las correspondientes operaciones, tendremos:
-\sqrt{2}\sqrt{2} + i\sqrt{2}\sqrt{2} = -2 + 2i
¡Como el resultado nos dio nuestro número complejo que nos da el ejercicio, entonces el número complejo -2 + 2i en la forma polar 2\sqrt{2} \left(\cos 135° + i \sin 135° \right) es correcta!
Gracias por estar en este momento con nosotros : )
Te recomiendo mucho el siguiente libro de álgebra:
Lehmann, C., (2012). Álgebra. México, DF, México: Editorial Limusa.
